Skip to content

Heap Problems

Questions discussed

Kth Largest Element in an Array (Medium)

Problem Statement

Given an integer array nums and an integer k, return the kth largest element in the array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Examples

Input: nums = [3,2,1,5,6,4], k = 2
Output: 5

Input: nums = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4

Constraints

  • \(1 \leq\) k <= nums.size() \(\leq\) \(10^4\)
  • \(- 10^4 \leq \text{nums[i]} \leq 10^4\)

Approach

  • There are several approaches, in which 2 are the most efficient:
    • use a k size min heap and put values into the heap until sequence runs out.
    • use the buildHeap() approach to build the given sequence into a heap, then remove top k times.
  • The first approach takes \(O(N)\) time and no extra memory.
  • The second approach takes \(O(N \log K)\) time and \(O(K)\) extra memory.
  • If you are given a sequence with no ending (data stream) then the second one will be the better approach.
  • Here in the solution we'll be using the second approach.
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int, vector<int>, greater<int>> minHeap;

        for (auto i:nums){
            if (minHeap.size() != k){
                // Until the min Heap is not of size `K` push elements
                minHeap.push(i);
            } else {
                // Now the min Heap is of size K. Push one element [it may be the kth largest]
                minHeap.push(i);

                // If not the kth largest it'll be removed
                // Otherwise the k-1th largest will be removed
                minHeap.pop();
            }
        }

        return minHeap.top();
    }
};

Find all K Largest Elements in the array

Problem Statement

This problem is a bit different than the previous one. Here you have to return K largest elements from a given sequence. For example

flowchart LR
    10-->12
    12-->13
    13-->167
    167-->46
    46-->2157

For the above sequence the \(K = 3\) largest elements should be the following: 

flowchart LR
    2157-->167-->46

Approach

  • From the above code if we look closely enough, we find that after all the operations done the remaining elements in the k sized heap contains all the elements that are greater or equal to the \(K^{\text{th}}\) largest element in the given sequence.
  • So return all the elements from the heap.

C++ Code

std::vector<int> kLargestElements(std::vector<int> &vector, int k){
    std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;

    std::vector<int> out;

    for (auto element:vector){
        if (minHeap.size() != k){
            minHeap.push(element);
        } else {
            minHeap.push(element);
            minHeap.pop();
        }
    }

    while (!minHeap.empty()){
        out.push_back(minHeap.top());
        minHeap.pop();
    }

    return out;
}

Sort a K Sorted array

Problem Statement

Each element in the array must be within the range k from it's desired position, Now sort the array as efficiently as possible.

Approach

  • For each index, the corresponding sorted element is in the array is within k to the left and k to the right of that index.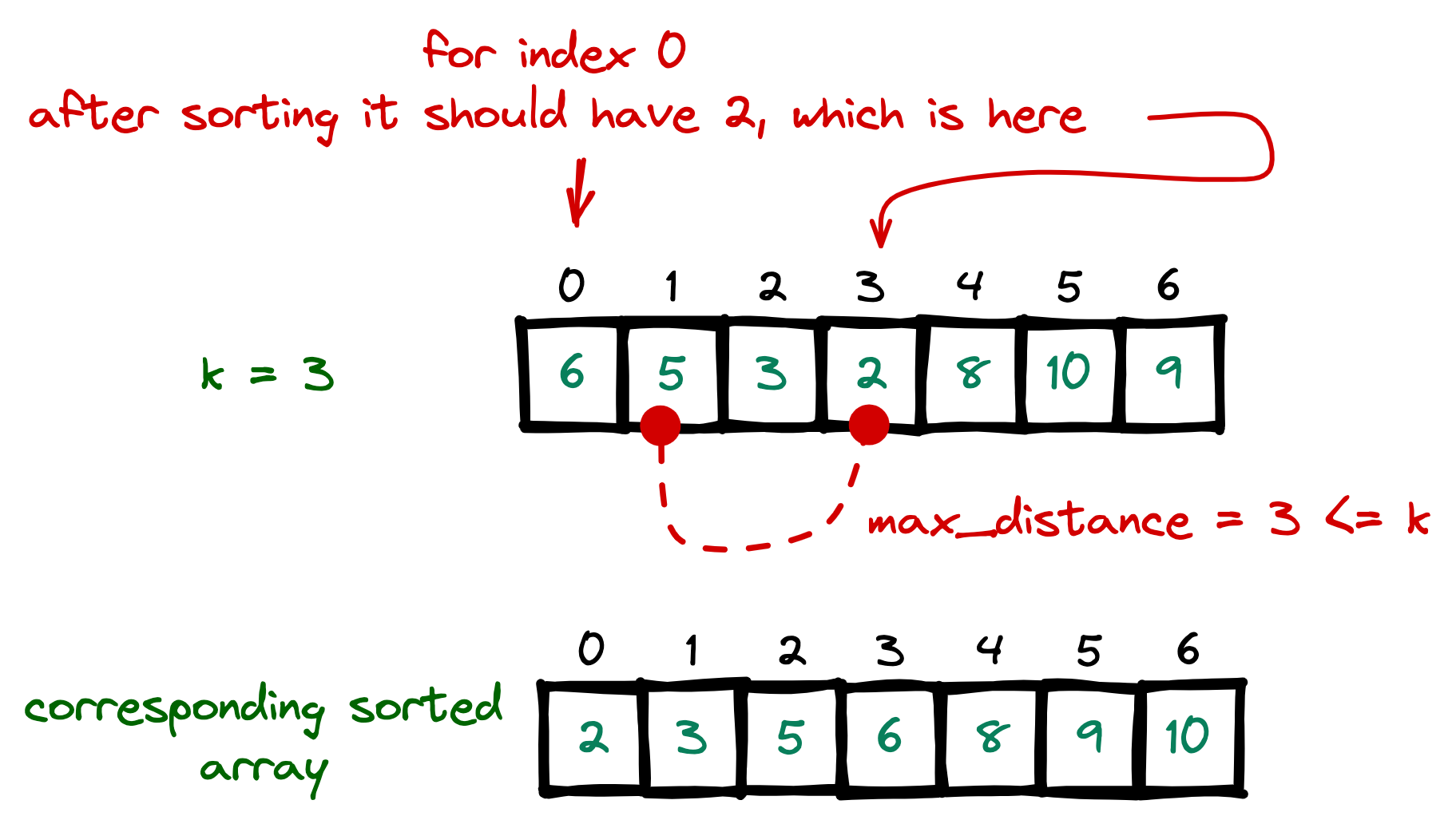 image
  • Now we make a min-heap of size k+1,
  • Now we push first k+1 elements into the heap.
  • Now for each index extract the min, then slide the window by 1 distance adding the \((k+1) + 1^{th}\) element to the heap and remove the min element from the min heap.
  • In the next step do the same with \((k+1) + 2^{th}\) element, unitl this pointer reaches to the end.
  • At the end extract the remaining min elements from the heap and add it to the out vector.
#include <iostream>
#include <queue>
#include <vector>

/*
    🗿 Implementation for sorting a k sorted array using heap 🗿
    🗿 Input is given a k sorted array [🗿 pass by address 🗿]
    🗿 returns the sorted array.
*/
std::vector<int> kSortedArray(std::vector<int> &array, int k) {
    int size = array.size();
    int index = 0;

    std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
    std::vector<int> out;

    // initially push k element into the min heap
    int nextuptoK = k + 1;
    while (nextuptoK) {
        minHeap.push(array[nextuptoK]);
        nextuptoK--;
    }

    // Now move forward with the array and put one new element into the min heap and
    // pop last element from the min heap [the minimum]. This popped element is the minimum element
    // so put it into the out vector.

    int window_last = k+2;
    while (window_last != size) {
        out.push_back(minHeap.top());
        minHeap.pop();

        minHeap.push(array[window_last]);
        window_last++;
    }

    while(!minHeap.empty()) {
        out.push_back(minHeap.top());
        minHeap.pop();
    }

    return out;
}

Find K Closest Elements (Medium)

Problem Statement

Given a sorted integer array arr, two integers k and x, return the k closest integers to x in the array. The result should also be sorted in ascending order.

An integer a is closer to x than an integer b if:

  1. |a - x| < |b - x|
  2. |a - x| == |b - x| and a < b

Examples

Input: arr = [1,2,3,4,5], k = 4, x = 3
Output: [1,2,3,4]

Input: arr = [1,2,3,4,5], k = 4, x = -1
Output: [1,2,3,4]

Approach

  • One approach could be that we subtract x from each element of the array and return whose difference with \(x\) is in \(\{0 \to k\}\)
  • Other approach would be to use a heap. Like the previous problem we pushed K largest or smallest elements into the array. Here what we'll do is
    • Make a minHeap,

Top K Frequent Elements (Medium)

Problem Statement

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Examples

Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]

Input: nums = [1], k = 1
Output: [1]

Constraints

  • 1 <= nums.length <= 105
  • k is in the range [1, the number of unique elements in the array].
  • It is guaranteed that the answer is unique.

Follow up: The algorithm's time complexity must be better than \(O(n \log n)\), where n is the array's size.

Approach

Code

Top K Frequent Elements

Find the problem on Leetcode \(\to\)

Problem Statement

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order

Example

Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]

Input: nums = [1,12,2,34,124,124,12,31,23,123,12,312,3,123,123,123,12,31,23,123,123]
and k = 5
Output: [123,12,23,31,124]

Approach

  • First we should make an unordered map to find the frequency of all the elements. We do not get that information by just looking at the elements of the array.
  • After that once we have the frequency of all the elements, we'll push elements on to a min heap of size \(K\) based on the frequency of those elements.
  • Making the size of the min heap limited to size \(K\) helps to keep track only the k most frequent elements, once we have a less frequent element, as it'll on the top of the min heap, we'll perform a heap pop.

Code

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        // first count all the elements and their occurences
        unordered_map<int, int> map;

        for (auto i:nums){
            if(map.find(i) == map.end()) {
                map.insert({i, 1});
            } else {
                map[i]++;
            }
        }

        // now that we have all the counts we'll do a quick heap implementation
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> minHeap;

        for (auto it=map.begin(); it!=map.end(); it++) {
            minHeap.push({
                it->second, it->first
            });

            if (minHeap.size() > k) {
                minHeap.pop();
            }
        }

        // at the end we have top k elements in the minHeap
        vector<int> answer;

        while(!minHeap.empty()) {
            answer.push_back(minHeap.top().second);
            minHeap.pop();
        }

        return answer;
    }
};

K Closest Points to Origin

Find the problem on leetcode \(\to\)

Problem Statement

Given an array of points where \(\text{points(i)} = [x_i, y_i]\) represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., \(\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\))

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

Approach

  • We'll use max heap to store the distant points from the origin.
  • To know how much distance they are in we'll make some ID system for each of the points, and calculate the distance between that point and the origin then put it in a hash table along with the ID,
  • Now we'll for each entry in the hashtable we'll put the entry in a max heap (with priority being the distance to the origin), if the max heap size if greater than \(k\) then we'll pop from the heap,
  • at last we'll get all the point's IDs remaining in the priority queue and return them via a ID to point lookup.

Code

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        vector<int> origin = {0,1};

        // make an ID System to identify each of the points
        // let's say their index in the points array is their ID

        // making map of point IDs and their distance to the origin
        // ID -> distance map
        unordered_map<int, float> distances;

        for (int i=0; i<points.size(); i++) {
            float distance = sqrt(points[i][0] * points[i][0] + points[i][1] * points[i][1]);
            distances.insert({i, distance});
        }

        // now make a priority queue to store the order and at last find k closest points
        // using a max heap we can do that

        priority_queue<pair<float, int>> pq; // Max Heap

        for (auto v:distances) {
            int id = v.first;
            int distance = v.second;

            pq.push({v.second, v.first});

            if (pq.size() > k) {
                pq.pop();
            }
        }

        // now the last k means the k closest points are remaining in the pq
        vector<vector<int>> answers;

        while (not pq.empty()) {
            auto top = pq.top();
            pq.pop();

            vector<int> v = {points[top.second][0], points[top.second][1]};
            answers.push_back(v);
        }

        return answers;
    }
};

Comments

This comments system is powered by GitHub Discussions