Problems on arrays
Questions discussed
- Single Number
- Dutch National Flag Partitioning
- String Compression Problem
- Best Time to Buy and Sell Stock
- Best Time to Buy and Sell Stock II
- Insert Interval
- Missing Number
- Majority Element
- Rotate Array
- How Many Numbers Are Smaller Than the Current Number
- Sort Array By Parity
- Replace Elements with Greatest Element on Right Side
- Sort colors
- Set matrix zeros
- Leaders in an array
- Count the number of inversions in an array
- Rotate Image
- Product of Array Except Self
- Two Sum II Input Array Is Sorted
- Container With Most Water
- Rain water trapping
- Two Sum IV
- Valid Sudoku
- Sort the Array
- Greatest Common Divisor of Strings
Single Number
Problem Statement
Given a non-empty array of integers nums, every element appears twice except for one. Find that single one. You must implement a solution with a linear runtime complexity and use only constant extra space.
Approach
If the problem was given in a sorted array we can implement this binary search approach. But here the array is not sorted. We can use a dictionary but it'll take more space.
Only other way of solving this problem is to use XOR operations. For each element in the array if we XOR them with each other we can find the odd one out.
Code
class Solution {
public:
int singleNumber(vector<int>& nums) {
int start = nums.front();
for (int i=1; i<nums.size(); i++) {
start ^= nums[i];
}
return start;
}
};
Dutch National Flag Partitioning
Problem Statement
Implemented naively, quicksort has large run times and deep function call stacks on arrays with many duplicates because the subarrays may differ greatly in size. One solution is to reorder the array so that all elements less than the pivot appear first, followed by elements equal to the pivot, followed by elements greater than the pivot. This is known as Dutch national flag partitioning, because the Dutch national flag consists of three horizontal bands, each in a different color.
Solution Pattern
- Main thing to do in this problem is to make groups of elements whose values are less, equal, more than the target.
- For \(O(N)\) space solutions we can create three new arrays called
less, more, equaland put values into it during the traversal. - For \(O(1)\) space solutions we can do these steps:
- Do - inplace grouping of all the less than target elements during the first pass,
- Do - inplace grouping of all the greater than target elements during the next pass. During this pass if we find one element that is greater than the target we can say that "Hey! we have entered into the
lesssubarray", so we can break out of the loop. - Total time complexity is \(O(N)\) for the first pass and on an avarage \(O(\frac{N}{2})\) in the second pass. Total of \(O(N)\).
def dutch_flag_partition(pivot_index: int, A: list[int]) -> None:
pivot_value: int = A[pivot_index]
small: int = 0
# Group all the smaller elements together at the start
# This is in-place grouping of elements smaller than some target
for i in range(len(A)):
if A[i] < pivot_value:
A[small], A[i] = A[i], A[small]
small += 1
# Group all the larger elements together at the end
larger: int = len(A) - 1
for i in reversed(range(len(A))):
if A[i] < pivot_value:
break
elif A[i] > pivot_value:
A[i], A[larger] = A[larger], A[i]
larger -= 1
Test Cases
- Test PASSED (204/204) [ 8 ms]
- Avarage running time: 65 us
- Median running time: 13 us
Similar problems
Given an array of n objects with keys that takes on of four values, reorder the array so that all the objects that have the same values appear together. \(O(1)\) space and \(O(N)\) time.
String Compression Problem
Problem Statement
Implement a method to perform basic string compression, like "aaaabbbcccaa" \(\to\) "a4b3c3a2"
Approach
- Make a one key dictionary. Add and count the subsequent characters, for C++ you'd make a
pair<int, int>and destroy it once a new character is seen, - Once you find a new element then drop the key, add the contents to the builder string and count again.
Code
def string_compressing(string: str) -> str:
build_string: list[str] = [] # using character array instead of string for O(1) append
dictionary: dict[str, int] = {}
for character in string:
if character in dictionary:
dictionary[character] += 1
elif character not in dictionary:
if dictionary != {}:
# If the dictionary is not empty means we have a new element to consider.
# Dump the contents to the build_string and make the dictionary = {}
build_string.append(list(dictionary.keys())[0])
build_string.append(str(dictionary[list(dictionary.keys())[0]]))
dictionary = {}
# Set the new character count to 1
dictionary[character] = 1
build_string.append(list(dictionary.keys())[0])
build_string.append(str(dictionary[list(dictionary.keys())[0]]))
build_string = "".join(build_string) # This does not take O(N^2), takes only O(N) to concatenate a character array to a string.
build_string = build_string.replace("1", '') # O(N)
return build_string
Time complexity
This solution take \(O(N)\) time and constant space if you don't count the return string. It uses space to hold an one key dictionary and the return string.
Best Time to Buy and Sell Stock
Problem Statement
You are given an array prices where prices[i] is the price of a given stock on the \(\text{i}^{\text{th}}\) day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return \(0\).
Examples
Example 1
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
Approach
- We start with the lowest profit possible which is \(0\),
- We'll start the analysis from day \(1\) not from day \(0\),
- We indicate the dip is the day \(0^{th}\) price. If we buy at that price then we analyse further.
- Now we analyze from day \(1 ... N\)
- For day \(1\) if we sell that stock the profit will be
profSLT = prices[1] - dipat the lowest dip so far, we update the max profit by taking thestd::maxof previous maximum profit and todays profit. - If todays price is lower than the last day's price, it is possible that we can get a better solution (profit) if not we already have stored the last best profit.
- We repeat this until we reach the last day.
- For day \(1\) if we sell that stock the profit will be
Code
class Solution {
public:
int maxProfit(vector<int>& prices) {
int mprof = 0; // maximum profit
int dip = prices[0]; // should buy at lowest dip starting from day 1
for (int i=1; i<prices.size(); i++) {
// profit if sold today bought at the lowest dip so far;
int profSLT = prices[i] - dip;
// if this is the maxprofit then update
mprof = std::max(mprof, profSLT);
if (prices[i] < dip) dip = prices[i];
}
return mprof;
}
};
Best Time to Buy and Sell Stock II
Problem Statement
Similar to the previous problem, you are given an integer array prices where prices[i] is the price of a given stock on the ith day.
On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.
Find and return the maximum profit you can achieve.
Approach
Similar to the previous problem we'll continue to implement the logic but, if we see a dip later in the future, we'll sell off and buy at tomorrows dip to avoid any potential loss.
Note
Here profitInCurrentWindow in the code denotes the profit in the current window. An window is reset when we sell off the stock because there will be a dip in the next day. We start the window by buying the stock in the next dip.
Code
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 1) return 0;
int totalProfit = 0;
int dip = prices[0];
int profitInCurrentWindow = 0;
// start from day 1 and local dip so far is day 0's price
for (int index = 1; index < prices.size(); index++) {
// today's price = prices[index]
int price = prices[index];
// see if selling today entails profit?
int profit = price - dip;
// what is the max profit possible in the current window
profitInCurrentWindow = std::max(profitInCurrentWindow, profit);
// if it is profitable and tomorrow's price goes down don't hold, sell and exit
// and reset the problem to next day and start again
if (profit > 0 and index < prices.size() - 1) {
if (prices[index + 1] < prices[index]) {
totalProfit = totalProfit + profitInCurrentWindow;
// also reset the dip to the index + 1
// for a new profit calculation for tomorrow
dip = prices[index + 1];
index++; // we reset the entire problem and recalculate everything from the next index
profitInCurrentWindow = 0; // reset the profit in the window
}
}
if (price < dip) dip = price;
}
totalProfit += profitInCurrentWindow; // update the last profit window
return totalProfit;
}
};
Insert Interval
Same Problem on Leetcode \(\to\)
Problem Statement
You are given an array of non-overlapping intervals intervals where \(\text{intervals}[i] = [\text{start}_i, \text{end}_i]\) represent the start and the end of the ith interval and intervals is sorted in ascending order by starti. You are also given an interval \(\text{newInterval} = [\text{start}, \text{end}]\) that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return intervals after the insertion.
Examples
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
Missing Number
Find the problem on Leetcode \(\to\)
Problem statement
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
Example
Input: nums = [3,0,1]
Output: 2
Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3].
2 is the missing number in the range since it does not appear in nums.
Approach
- There can be several approaches, one of which is sorting then find what's missing?
- There is also another approach where you sum up all the numbers (using \(\frac{n(n+1)}{2}\)) then subtract from elements present in the array. This is a \(O(N)\) and constant space solution. But using this is risky because if \(n\) is anywhere large enough to \(\text{INT_MAX}\) then there is a high probability that \(\frac{n(n+1)}{2}\) overflows. So it is not recommended to use this approach instead use the following one:
- There is another approach where you use XOR operations to find the missing elements. I have written all the code for all the approaches below. Here is no chance of integer overflow or anything. For XOR apporach you first have to find the XOR of elements from \(\{1 \to n\}\) then find the XOR of elements present in the array. Now XOR between these two is the missing element so return it.
Code
Using sorting method
class Solution {
public:
int missingNumber(vector<int>& nums) {
std::sort(nums.begin(), nums.end());
int index = 0;
for (auto i:nums) {
if (i != index) return index;
index++;
}
return index;
}
};
Using sum and substraction method
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
int sum = n*(n+1) / 2;
for (int i:nums) sum -= i;
return sum;
}
};
Using XOR Method
class Solution {
public:
int missingNumber(vector<int>& nums) {
int l1 = 0; // contains xor of 1 to n
int l2 = nums[0]; // contains xor of all the nums elements
for (int i=0; i <= nums.size(); i++) {
l1 ^= i;
}
for (int j=1; j<nums.size(); j++) {
l2 ^= nums[j];
}
return l1^l2;
}
};
Majority Element
Problem Statement
Given an array nums of size n, return the majority element.
The majority element is the element that appears more than \(\lfloor\frac{n}{2}\rfloor\) times. You may assume that the majority element always exists in the array.
Approach
- One approach is to use a dictionary to implement a counter for each element. Then find what is \(\gt \lfloor\frac{n}{2}\rfloor\), but it'll take extra \(O(n)\) space. So we need to find a new approach.
- There is an algorithm called boyer moore majority voting algorithm, using that we can easily find the majority element in the array.
Boyer Moore Algorithm
Boyer–Moore majority vote algorithm can find the majority of a sequence of elements using linear time and constant space if exists. The returned result may not be the majority element (if not exists), so we have to do an additional check if the indicated element indeed the majority element.
The algorithm goes like this:
- Initialize an element majority and a counter
counterwithcounter = 0 - For each element x of the input sequence:
- If
counter = 0, then assign majority as x andcounter = 1 - If you encounter next the same element as the majority element you increment the counter.
- Otherwise decrease the counter and no change to the majority element.
- If
- at the end return the
majorityvariable. It may be or may not be the majority element (if it doesn't exists) then we need check if that is the majority element with just a single pass.
Example
Let's run the algorithm on an example to see how this is working
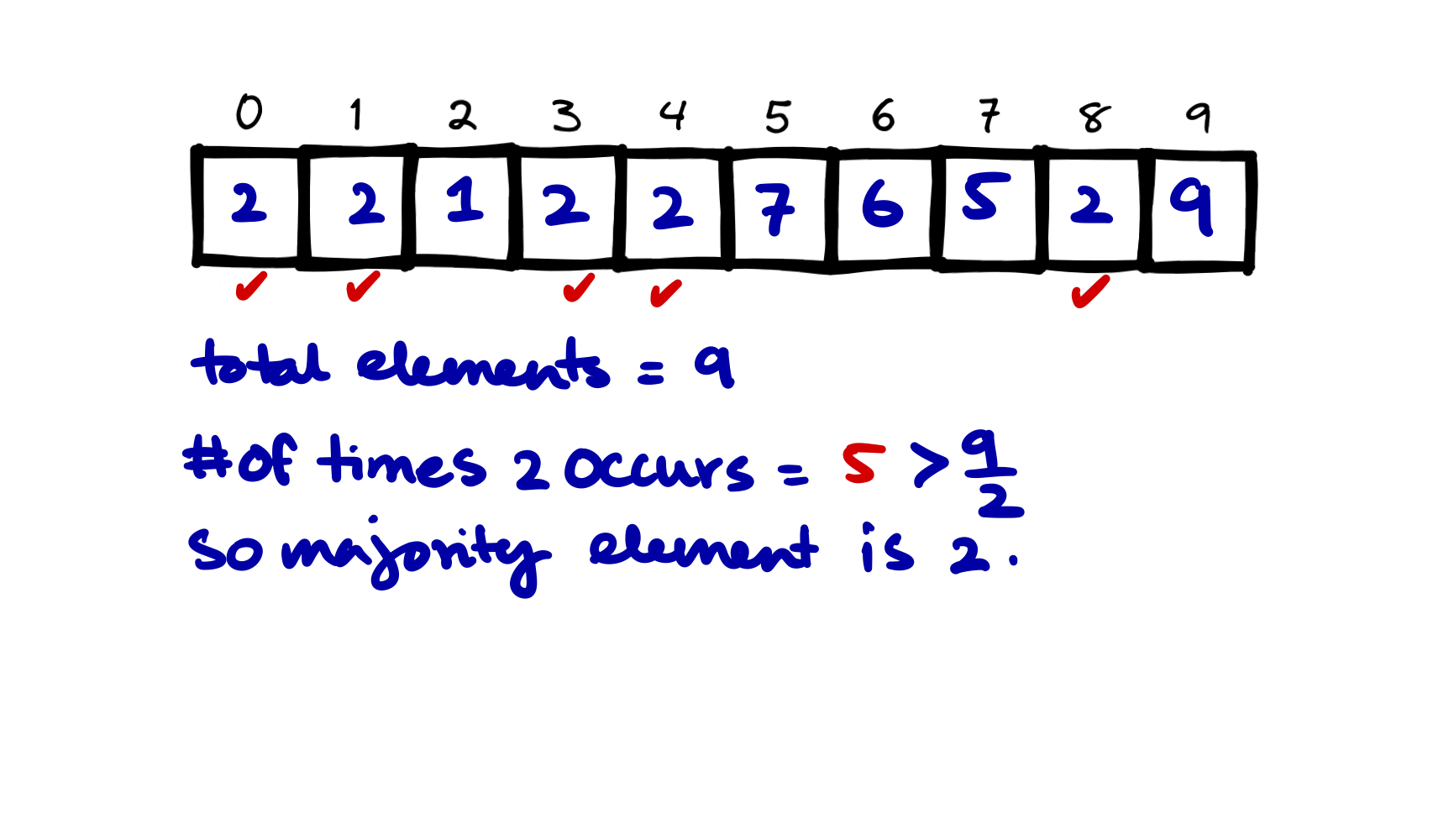
Running the algorithm on the example
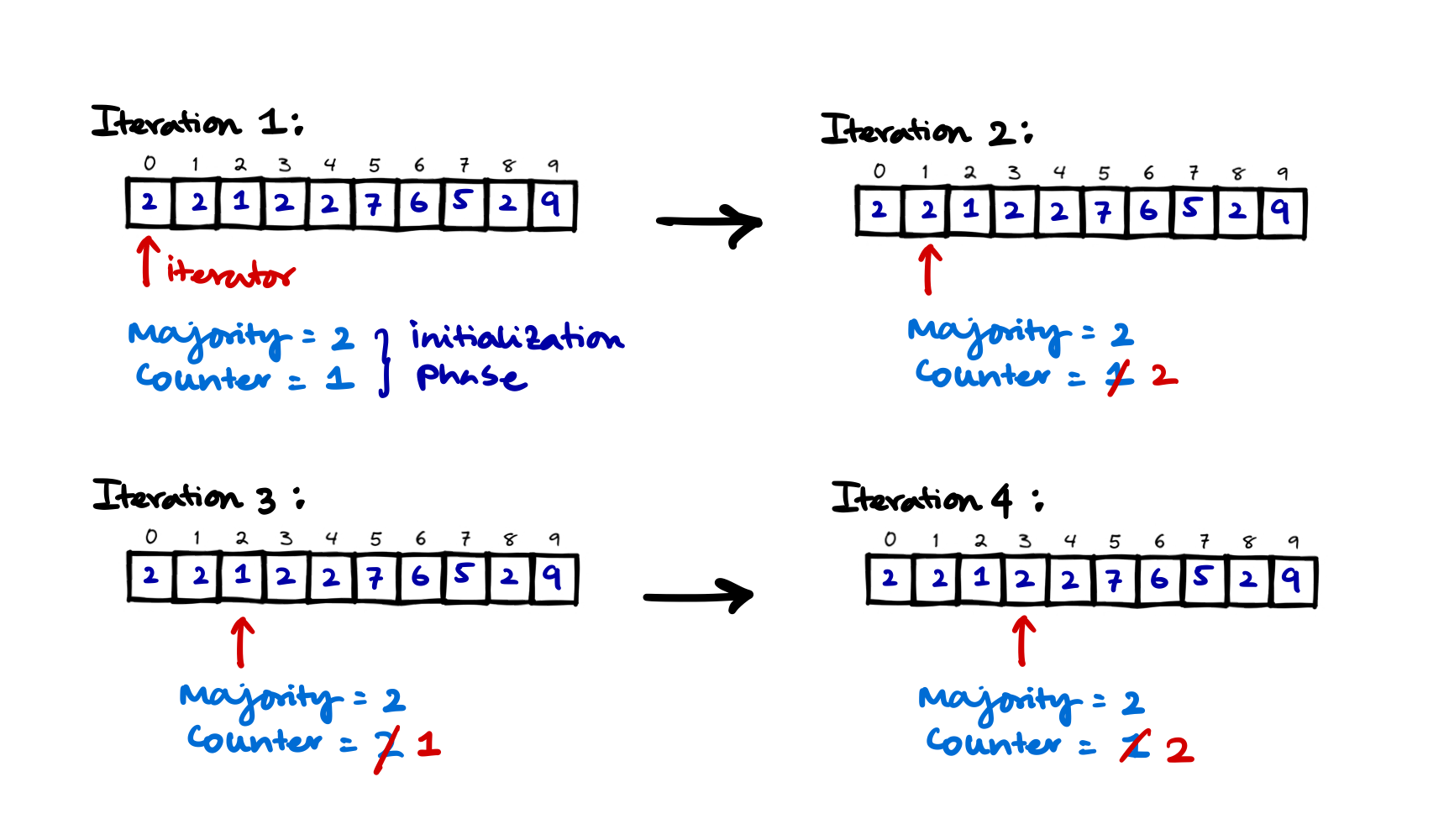
Iteration 1 to 4
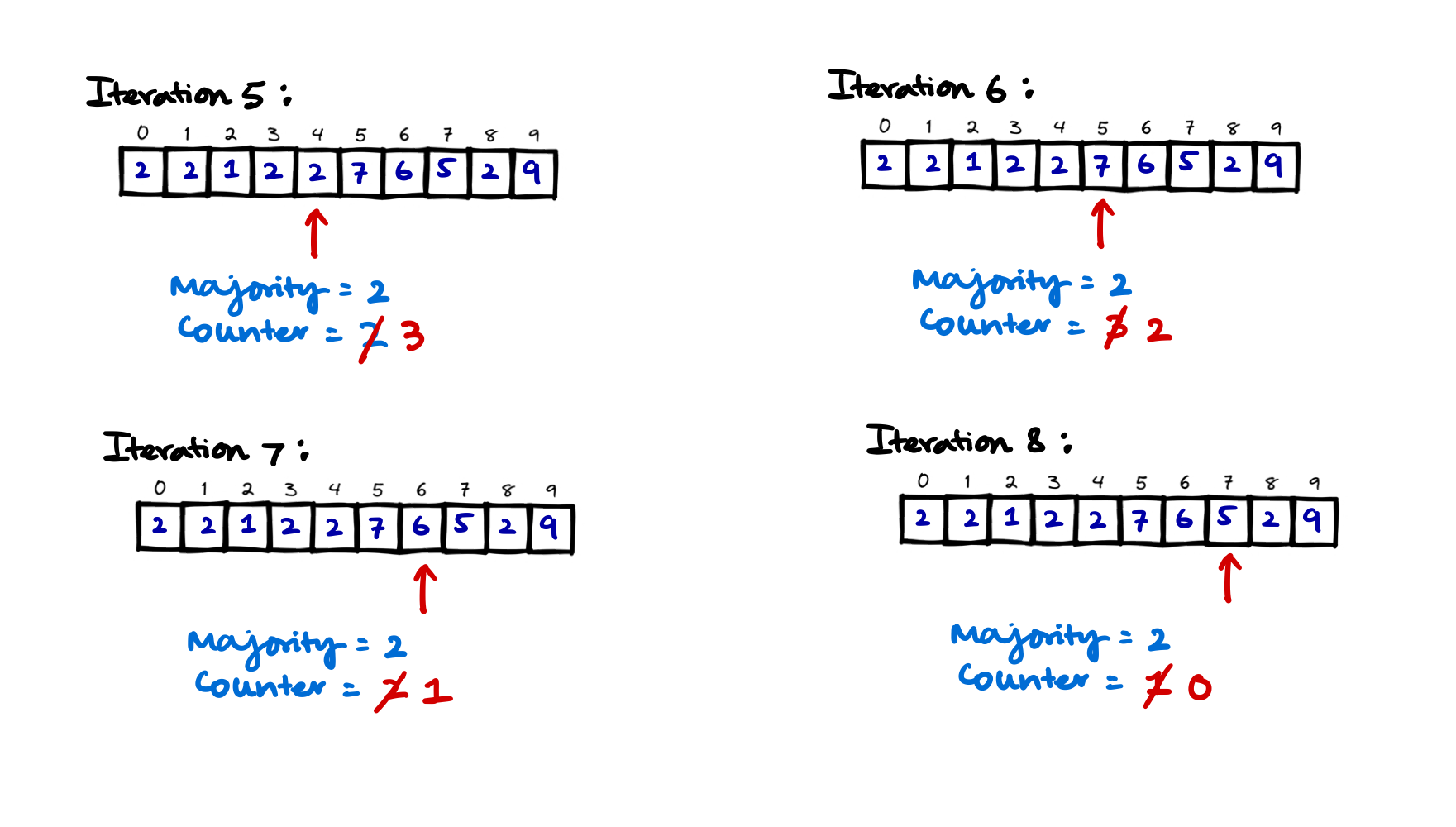
Iteration 5 to 8
Iteration 9 and 10
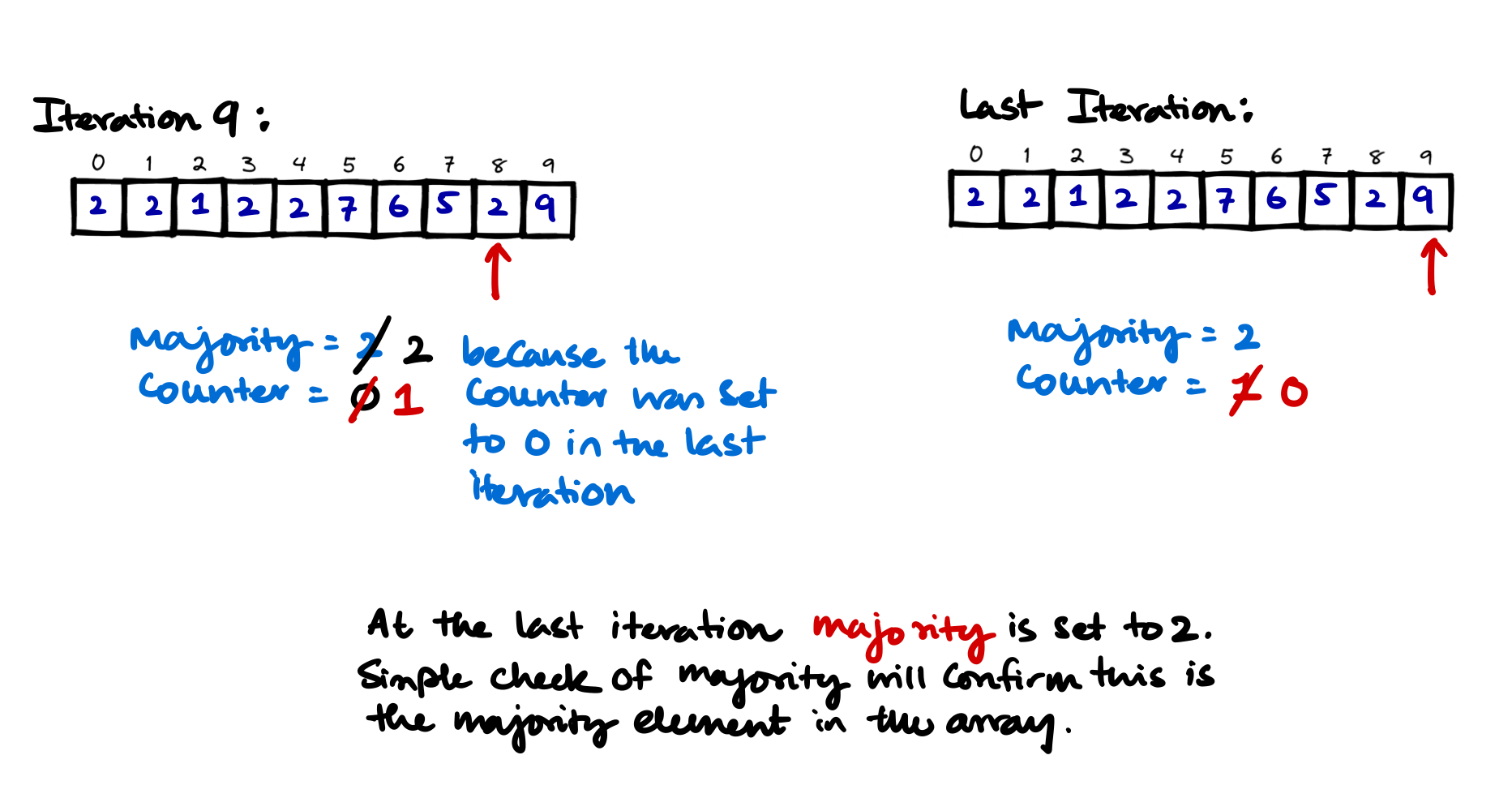
At the very end the majority variable may or may not contains the majority element. We need check if that is the majority element with a single pass on the array to count up the number of occurrences of the element indicated in majority variable.
Code
class Solution {
public:
int majorityElement(vector<int>& nums) {
int counter = 0;
int majority = 0;
for (int i:nums) {
if (counter == 0) {
majority = i;
counter += 1;
} else {
if (i == majority) {
counter++;
} else {
counter--;
}
}
}
return majority; // we assume that the majority element always exists in the array
}
};
Rotate Array
Problem Statement
Given an array, rotate the array to the right by k steps, where k is non-negative in constant space and linear time.
Examples
Input: nums = [1,2,3,4,5,6,7], k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]
Input: nums = [-1,-100,3,99], k = 2
Output: [3,99,-1,-100]
Explanation:
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]
Several approaches with C++ code
Not so much of an optimized approach, will fetch you a TLE. But for understanding it is a great apporach. We convert the k rotation problem into a subproblem of rotationOnce() for k times. We implement the rotationOnce() subroutine like this:
- See the last element, store it in
lastvariable. - then for element of index starting from \(\text{last} - 2\) down to \(0\) swap it with the next element, to shift it by one,
- at last swap the first element (\(0^{th}\) index element with the
lastvariable). - This is how you rotate by one element.
- Do this K times to solve the problem. Total time complexity is \(O(kn)\), so we'll get TLE in the compiler. This is a polynomial in \(n\) and \(k\). But \(k\) can be \(2^n\) so overall this is not efficient. We can reduce the number of subroutine calls down to \(k \text{mod} n\) but if \(n\) is large enough and \(k\) is almost \(n\) then the problem of TLE again occurs.
Here is a code using this approach
class Solution {
private:
void rotateOnce(vector<int>& nums) {
int last = nums.back();
int size = nums.size();
for (int i=size-2; i>=0; i--) {
nums[i+1] = nums[i];
}
nums[0] = last;
}
public:
void rotate(vector<int>& nums, int k) {
int rotations = k % nums.size();
while(rotations) {
rotateOnce(nums);
rotations--;
}
}
};
The code here will not run in a reasonable amount of time for a sufficiently large input size. So we have to design some better algorithms.
Using Extra space (a faster algorithm in linear time)
Instead of using the rotate once subroutine we can store all the last k elements in some temporary array, then instead of shifting one element once to the right and putting the last element to the front we can
- push those elements k step ahead
- put last k elements to the front of the array.
This way the time complexity becomes linear time in \(O(n + k)\). This does not give TLE. But this takes \(O(k)\) extra space.
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k = k % nums.size();
int size = nums.size();
vector<int> temp(nums.end()-k, nums.end());
// for all the elements starting from
// size - k - 1 down to 0 write it k space ahead
for (int i=size-k-1; i>=0; i--) {
nums[i + k] = nums[i];
}
int start = 0;
for (auto t:temp) {
nums[start] = t;
start++;
}
}
};
Without extra space and linear time complexity in \(n\)
There is a very ingenious solution to the problem. I'll explain this with diagrams and will give you an working C++ code.
Approach
The approach to get the solution goes like this:
- inplace reverse the array from last to \(k\),
- then inplace reverse the array from start to
size - k - now reverse the whole array.
Dry run on some example
Example array
 Dry run on that example
Dry run on that example

Code
class Solution {
private:
void inplace_reverse(vector<int>& nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
public:
void rotate(vector<int>& nums, int k) {
k = k % nums.size();
int size = nums.size();
inplace_reverse(nums, size-k, size-1);
inplace_reverse(nums, 0, size-k-1);
inplace_reverse(nums, 0, size-1);
}
};
How Many Numbers Are Smaller Than the Current Number
Problem Statement
Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j's such that j != i and nums[j] < nums[i].
Return the answer in an array.
Approach
The most straight forward approach is to implement this by sorting and binary searching the lower bound for each element in the array. First we sort the array. The amount of element that is lower than each element in the array is actually equal to the lowerbound on the sorted array.
Using a non comparison based sorting algorithm we can reduce the time complexity even further down to \(O(n)\).
Code
class Solution {
private:
int lower_bound(vector<int> &nums, int target) {
int start = 0;
int end = nums.size() - 1;
int middle = start + (end - start) / 2;
while (start < end) {
if (nums[middle] == target) end = middle;
if (nums[middle] < target) start = middle + 1;
if (nums[middle] > target) end = middle - 1;
middle = start + (end - start) / 2;
}
return start;
}
public:
vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
vector<int> v(nums.begin(), nums.end());
vector<int> answers;
sort(v.begin(), v.end());
for (int i:nums) {
int lb = lower_bound(v, i);
answers.push_back(lb);
}
return answers;
}
};
Sort Array By Parity
Problem Statement
Given an integer array nums, move all the even integers at the beginning of the array followed by all the odd integers.
Approach
We'll use the in-place gathering algorithm to gather all the even numbers at the begining of the array. The in-place gathering algorithm is explained in the following video. It's a super useful gathering algorithm that gathers elements of an array based on some condition. In the video I have explained two different scenarios where this gathering algorithm can be used.
Code
class Solution {
public:
vector<int> sortArrayByParity(vector<int>& nums) {
int even = 0;
// gathering all the even integers
for (int i=0; i<nums.size(); i++) {
if (nums[i] % 2 == 0) {
int temp = nums[i];
nums[i] = nums[even];
nums[even] = temp;
even++;
}
}
return nums;
}
};
Replace Elements with Greatest Element on Right Side
Problem Statement
Given an array arr, replace every element in that array with the greatest element among the elements to its right, and replace the last element with -1.
After doing so, return the array.
Example
Input: arr = [17,18,5,4,6,1]
Output: [18,6,6,6,1,-1]
Explanation:
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
Approach
- One approach is to for each element find the maximum element from that element to the last of the aray, obviously this will take \(O(n^2)\) time which is not optimal.
class Solution { public: vector<int> replaceElements(vector<int>& arr) { vector<int> answer; int _max = -1; for (int i=0; i<arr.size();i++) { if (_max == arr[i]) _max = -1; // find the max from it's right for (int j=i + 1; j<arr.size(); j++) { _max = std::max(_max, arr[j]); } answer.push_back(_max); } return answer; } }; - Instead we'll use an ingenious way, we'll travel from the last to the begining of the array, first we'll make the maximum element to the right as \(-1\), then we'll record the maximum element so far and go left to the beginning of the array.
- This will return the reverse of the intended result. At the end we'll reverese the elements in the array in-place.
Code
Extra space solution
class Solution {
public:
vector<int> replaceElements(vector<int>& arr) {
vector<int> answer;
int _max = -1;
answer.push_back(_max);
_max = arr.back();
for (int i=arr.size() - 2; i>=0; i--) {
answer.push_back(_max);
_max = std::max(_max, arr[i]);
}
std::reverse(answer.begin(), answer.end());
return answer;
}
};
class Solution {
public:
vector<int> replaceElements(vector<int>& arr) {
int _max = -1;
int back = arr.back();
for (int i=arr.size()-1; i>0; i--) {
// update with the max we've seen so far
arr[i] = _max;
// check if the current element is max or not?
_max = std::max(back, _max);
// as we're updating `a[i]` we should hold the value
// in `back` variable and go left to the array
back = arr[i - 1];
}
arr[0] = _max;
return arr;
}
};
Sort colors
Problem Statement
Given an array nums with n objects colored red, white, or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers 0, 1, and 2 to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
Approach
This problem is the prime example where we should be using the in-place grouping algorithm. Using that we first group zeros with condition elements being less than \(1\) to the left of the array and then group 2's with condition elements being greater than \(1\) to the right of the array. All the ones would be sandwitched between 0s and 2s.
This is how the array becomes sorted without the usage of sorting function.
Code
class Solution {
public:
void sortColors(vector<int>& a) {
// inplace gathering algorithm
// gather all 0 to the left of the array
int last = 0;
int n = a.size();
for (int i = 0; i < n; i++) {
if (a[i] == 0) {
swap(a[last], a[i]);
last++;
}
}
// gather all 2 to the right of the array
last = n - 1;
for (int i = n - 1; i >= 0; --i) {
if(a[i] == 2) {
swap(a[i], a[last]);
--last;
}
}
}
}
Set matrix zeros
Problem Statement
Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's. You must do it in place.
Example
Approach
- Do stuffs
Code
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
// setting 2 indicators
// one for rows to be updated
// one for columns to be updated
vector<int> r;
vector<int> c;
for (int i=0; i<matrix.size(); i++) {
for (int j=0; j<matrix[0].size(); j++) {
if(matrix[i][j] == 0) {
r.push_back(i);
c.push_back(j);
}
}
}
// set zeros
for (auto row:r) {
for (int c=0; c<matrix[row].size(); c++)
matrix[row][c] = 0;
}
for (auto col:c) {
for (int r=0; r<matrix.size(); r++)
matrix[r][col] = 0;
}
}
};
Leaders in an array
Problem on Coding Ninjas \(\to\)
Problem Statement
Given a sequence of numbers. Find all leaders in sequence. An element is a leader if it is strictly greater than all the elements on its right side.
Example
The given sequence is [13, 14, 3, 8, 2]
13 Not a leader because on the right side 14 is greater than 13.
14 lt is a leader because no one greater element in the right side.
3 Not a leader because on the right side 8 are greater than 3.
8 It is a leader because no one greater element on the right side.
2 It is a leader because it is the rightmost element in a sequence.
Hence there are 3 leaders in the above sequence which are 14, 8, 2.
Approach
- We'll traverse the array from right to left, set the max as the last element
- push the last element on the answer, then go forward
- if we find any element that is greater than the
current_maxmeans it is a leader because it is greater than anything we've seen from its right, - else just go backward without doing anything.
- At last in-place reverse the vector to get the result.
Code
void reverse_vector(vector<int>&v) {
int start = 0;
int end = v.size() - 1;
while (start < end) {
int temp = v[start];
v[start] = v[end];
v[end] = temp;
start++;
end--;
}
}
vector<int> findLeaders(vector<int> &elements, int n) {
// Write your code here.
vector<int> leaders;
int current_max = elements.back();
leaders.push_back(current_max);
for (int i=elements.size() - 2; i >= 0; i--) {
if (elements[i] > current_max) {
current_max = elements[i];
leaders.push_back(elements[i]);
}
}
reverse_vector(leaders);
return leaders;
}
Time and memory complexity
It takes total \(O(N)\) time and no extra space to run.
Count the number of inversions in an array
Find the problem on GeeksForGeeks \(\to\)
Problem Statement
Given an array of integers. Find the Inversion Count in the array.
Inversion Count: For an array, inversion count indicates how far (or close) the array is from being sorted. If array is already sorted then the inversion count is 0. If an array is sorted in the reverse order then the inversion count is the maximum.
Formally, two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j.
Examples
Input: N = 5, arr[] = {2, 4, 1, 3, 5}
Output: 3
Explanation: The sequence 2, 4, 1, 3, 5
has three inversions (2, 1), (4, 1), (4, 3).
Input: N = 5
arr[] = {2, 3, 4, 5, 6}
Output: 0
Explanation: As the sequence is already
sorted so there is no inversion count.
Input: N = 3, arr[] = {10, 10, 10}
Output: 0
Explanation: As all the elements of array
are same, so there is no inversion count.
Constraints
- Expected Time Complexity: \(O(n \log n)\).
- Expected Auxiliary Space: \(O(n)\)
Brute force Approach
- First we'll traverse from the end of the array to the first,
- for each element from \(\text{last} \to \text{first}\) we'll check what is the number of elements that are greater than this element, these are the inversions.
- This will obviously take \(O(n^2)\) time complexity which will result in some TLE for larger testcases.
Code for this approach
class Solution{
public:
// arr[]: Input Array
// N : Size of the Array arr[]
// Function to count inversions in the array.
long long int inversionCount(long long arr[], long long N) {
// Your Code Here
long long int inversions = 0;
long long int start = 0;
long long int end = N - 1;
while (end > start) {
for (int t=end - 1; t>=0; t--) {
if (arr[t] > arr[end]) {
inversions++;
}
}
end--;
}
return inversions;
}
};
Using this code passes 100 / 117 testcases in the gfg platform. So we need to optimize this further.
A More optimized approach
The following is a more optimized solution to find the number of inversions in the array, which takes a but lesser time so that we don't get any TLEs.
The number of inversions is a measure of how unsorted the array really is. So using some sorting properties we must derive at the number of inversions. It is also should be noted that in a sorted array the number of inversions is \(0\).
We'll use merge sort to do this. During the merge sort we'll run some subroutine that'll calculate the number of inversions. This will take \(O(n \log n)\) time which is faster than \(O(n^2)\). So understanding the merge sort is a critical component solving this problem.
Rotate Image
Problem Statement
You are given an \(N \times N\) 2D matrix representing an image, rotate the image by \(90°\) degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Approach
- This is essentially equivalent to an in-place transpose of the matrix
- then inplace reversal of each row of the matrix.
Code
class Solution {
private:
void transposeSubroutine(vector<vector<int>>& matrix) {
int end = matrix.size();
for (int i=0; i<end; i++) {
for (int j = i; j<end; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
void in_place_reversal(vector<vector<int>>& matrix, int row) {
int start = 0;
int end = matrix[row].size() - 1;
while(start < end) {
int temp = matrix[row][start];
matrix[row][start] = matrix[row][end];
matrix[row][end] = temp;
start++;
end--;
}
}
public:
void rotate(vector<vector<int>>& matrix) {
// rotating by 90* is essentially
// computing the transpose of the matrix
// then reversing all the arrays
transposeSubroutine(matrix);
// for each row do a inplace reversal
for (int i=0; i<matrix.size(); i++) {
in_place_reversal(matrix, i);
}
}
};
Product of Array Except Self
Problem Statement
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
Example
Approach using division operator
We can easily come up with a \(O(n)\) solution with \(O(1)\) memory complexity by just multiplying all the numbers of the array and divide them by the element at the current index. We should create provisions to handle Divide By Zero cases which you can see in the code below.
Code using division operation
class Solution {
private:
int findProductExceptIndex(vector<int>& nums, int index) {
int product = 1;
for (int i=0; i<nums.size(); i++) {
if (i != index) {
product *= nums[i];
}
}
return product;
}
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> result;
int prod = 1;
int zero_count = 0;
for (int i=0; i<nums.size(); i++) {
// to check if all are zero
if (nums[i] == 0) zero_count++;
// find the product of all
prod *= nums[i];
}
if (zero_count == nums.size()) {
// if all are zero
// directly return so no other computation is done
vector<int> v(zero_count, 0);
return v;
}
for (int j=0; j<nums.size(); j++) {
if (prod == 0) {
if (nums[j] == 0) {
// if this element is zero
// then find the product except self
// brutally
result.push_back(findProductExceptIndex(nums, j));
} else {
result.push_back(0);
}
} else {
result.push_back(prod / nums[j]);
}
}
return result;
}
};
Code for without the division approach
class Solution {
private:
void reverse_vector(vector<int>& nums) {
int start = 0;
int end = nums.size() - 1;
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
void prefixProd(vector<int>& nums, vector<int>&prefix) {
int prod = 1;
prefix.push_back(1);
for (auto i:nums) {
prefix.push_back(prod*i);
prod = prefix.back();
}
}
void postfixProd(vector<int>& nums, vector<int>&postfix) {
int prod = 1;
for (int i=nums.size() - 1; i>=0; i--) {
postfix.push_back(prod*nums[i]);
prod = postfix.back();
}
// reverse subroutine at the end to get the actual answer
reverse_vector(postfix);
postfix.push_back(1);
}
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> productExceptSelfOrder;
vector<int> prefix;
vector<int> postfix;
// build prefix and postfix products
prefixProd(nums, prefix);
postfixProd(nums, postfix);
// now that we have both the prefix products and postfix products
// it'll be easy to find the productExceptSelfOrder
for (int i=0; i<postfix.size() - 1; i++) {
int preprod = prefix[i];
int postprod = postfix[i+1];
productExceptSelfOrder.push_back(preprod * postprod);
}
return productExceptSelfOrder;
}
};
A Better in-place solution (most optimized)
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> answer;
int prod = 1;
answer.push_back(1);
for (int i=0; i<nums.size(); i++) {
answer.push_back(prod * nums[i]);
prod = answer.back();
}
answer.pop_back();
// our answer now holds all the prefix
// now instead of creating a new postfix array
// just do the postfix in place
prod = 1;
for (int j=nums.size() - 1; j >=1; j--) {
prod*= nums[j];
answer[j - 1] *= prod;
}
return answer;
}
};
Two Sum II Input Array Is Sorted
Find the Problem on Leetcode \(\to\)
Problem Statement
Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number. Let these two numbers be numbers[index1] and numbers[index2] where \(1 \le\) index1 < index2 \(\leq\) numbers.length.
Return the indices of the two numbers, index1 and index2, added by one as an integer array [index1, index2] of length 2.
The tests are generated such that there is exactly one solution. You may not use the same element twice.
The solution must use only constant extra space.
Approach
- Our approach will use a two pointer solution. We'll put a pointer
startat 0 andendat the end of the array. - Next we'll see if
sum < target, we must try to add some element greater than thearray[start]so that our sum reaches target. As the array is already sorted in non-decreasing order we'll move start by 1 to increment the sum upto target, - If
sum > targetmeans we overshoot the sum, so to reduce the sum down to target we'll decrementendby 1.
Code
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int start = 0;
int end = numbers.size() - 1;
int sum = numbers[start] + numbers[end];
if (sum == target) {
vector<int> v = {start + 1, end + 1};
return v;
}
while (sum != target and start < end) {
if (sum == target) break;
if (sum < target) {
start++;
}
if (sum > target) {
end--;
}
sum = numbers[start] + numbers[end];
}
vector<int> v = {start+1, end+1};
return v;
}
};
Container With Most Water
Find the problem on Leetcode \(\to\)
Problem Statement
You are given an integer array height of length \(n\). There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example
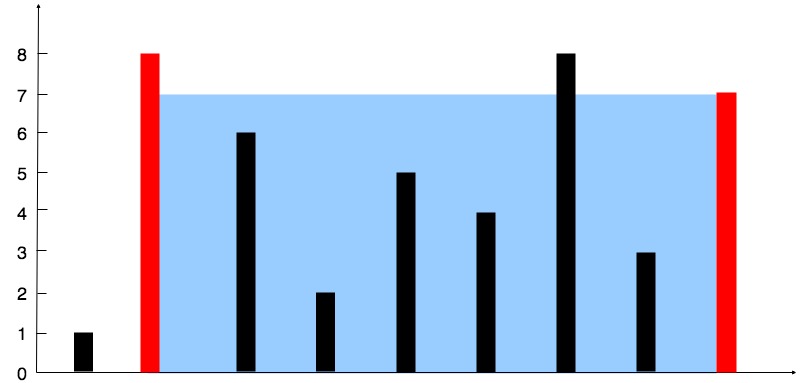
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7].
In this case, the max area of water (blue section) the container can contain is 49.
Approach
- [will be added soon]
Code
class Solution {
public:
int maxArea(vector<int>& height) {
int start = 0;
int end = height.size() - 1;
int water = 0;
while (start < end) {
int h = std::min(height[start], height[end]);
water = std::max(h * (end - start), water);
while(start < end and height[start] <= h) start++;
while(start < end and height[end] <= h) end--;
}
return water;
}
};
Rain water trapping
Same Problem on Leetcode \(\to\)
Problem Statement
Given \(N\) non-negative integers representing an elevation map where the width of each bar is \(1\), compute how much water it can trap after raining.
Example

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Explainer
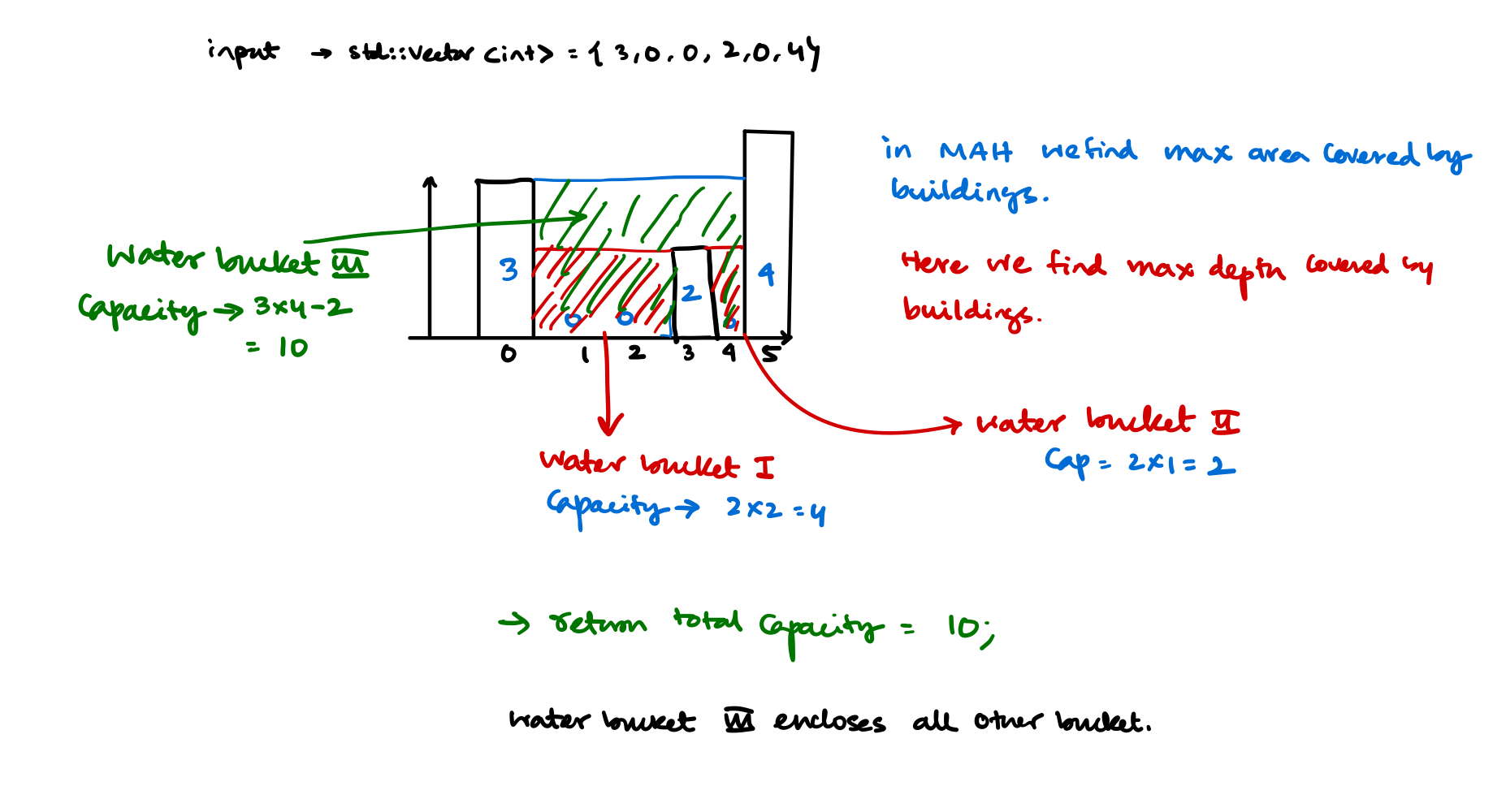
Approach
- For each building figure out how much water can be trapped on top of its roof.
- For all buildings add the water trapped on top of its roof.
- Return the total.
- To calculate how much water can be trapped on top of its roof, look left and see what is the largest building and look right and see what is the largest building. Get the smallest of those two. That should be the height of water on top of the building.
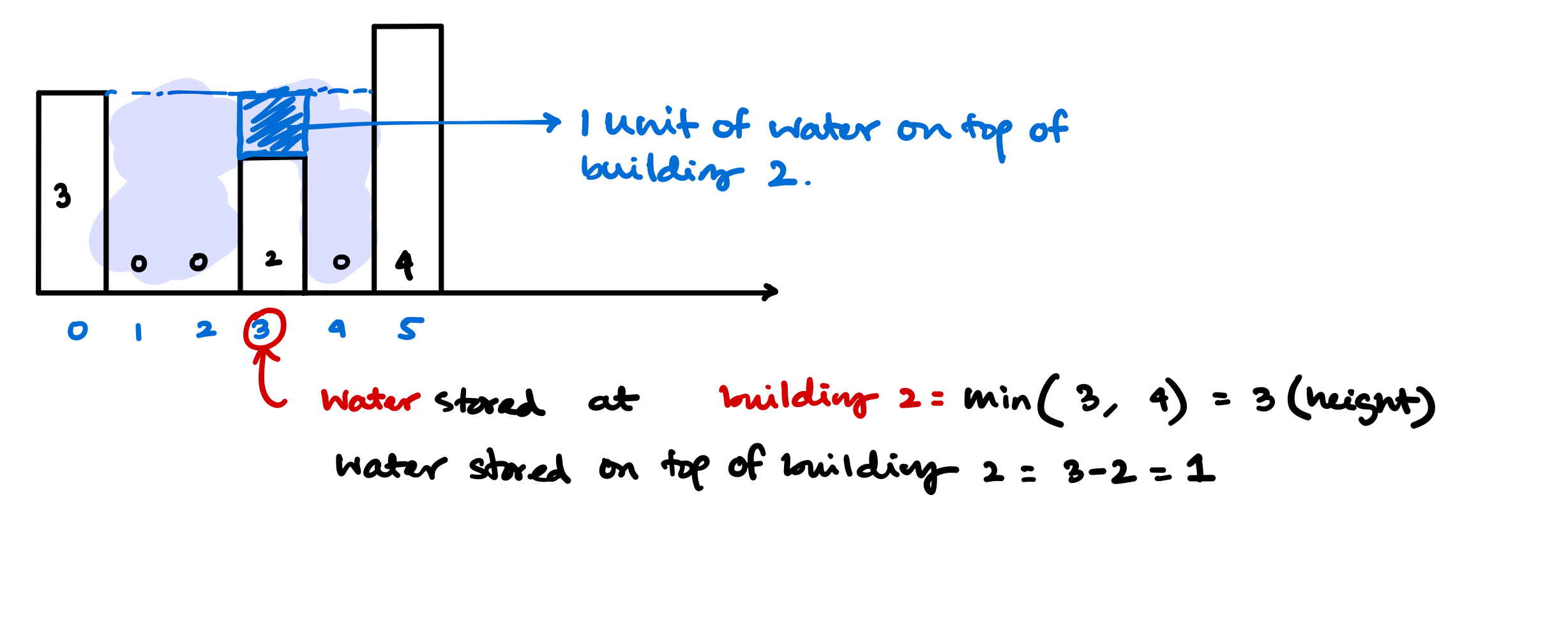
Solution
- For each building find the maximum height on both left and right sides,
- then take the minimum of those heights \(\to\) that should be the water height at that location.
- Subtract the height of the building from it to get how much water is stored on top of the building.
- For each building add up all the water stored on top of the roof.
- Return the sum as the total water stored in the system.
Code
class Solution {
private:
void _reverse(vector<int> &v) {
int start = 0;
int end = v.size() - 1;
while (start < end) {
int temp = v[start];
v[start] = v[end];
v[end] = temp;
start++;
end--;
}
}
public:
int trap(vector<int>& height) {
// for each index find the maximum boundary to the left
vector<int> left;
int currentMaxToLeft = 0;
for (auto i:height) {
if (i > currentMaxToLeft) {
left.push_back(currentMaxToLeft);
currentMaxToLeft = i;
} else {
left.push_back(currentMaxToLeft);
}
}
// for each index find the maximum boundary to the right
vector<int> right;
int currentMaxToRight = 0;
for (int i=height.size() - 1; i>=0; i--) {
if (height[i] > currentMaxToRight) {
right.push_back(currentMaxToRight);
currentMaxToRight = height[i];
} else {
right.push_back(currentMaxToRight);
}
}
_reverse(right); // reverse to sortout the order
// based on the left max and right max we find the minimum among this two
// (lower bound), then find the water on top of the building.
int water = 0;
for (int i=0; i<height.size() - 1; i++) {
// limiting height = min of left max and right max
int limiter = std::min(left[i], right[i]);
int waterOnTheBuilding = limiter - height[i];
if (waterOnTheBuilding > 0) water += waterOnTheBuilding;
}
return water;
}
};
Two Sum IV
Find the problem on leetcode \(\to\)
Problem Statement
Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.
Example
Approach
- We've previously solved the problem Two sum II where the input is sorted.
- Using 2 pointer approach we easily solved the problem, similar to that here if we do an inorder traversal we'll also get a sorted array,
- So the approach works like that, we first traverse in-order then use a 2 pointer approach to solve the 2 sum problem.
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> inOrder;
void build(TreeNode* root) {
if (root) {
build(root->left);
inOrder.push_back(root->val);
build(root->right);
}
}
public:
bool findTarget(TreeNode* root, int k) {
build(root);
// now 2 Sum II on the sorted list inOrder
int start = 0;
int end = inOrder.size() - 1;
int sum = inOrder[start] + inOrder[end];
while (start < end) {
if (sum < k) {
start++;
} else if (sum > k) {
end--;
} else if (sum == k) {
return true;
}
sum = inOrder[start] + inOrder[end];
}
return false;
}
};
Valid Sudoku
Problem Statement
Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits 1-9 without repetition.
- Each column must contain the digits 1-9 without repetition.
- Each of the nine 3 x 3 sub-boxes of the grid must contain the digits 1-9 without repetition.
Note A Sudoku board (partially filled) could be valid but is not necessarily solvable. Only the filled cells need to be validated according to the mentioned rules.
Approach
- We'll have three subroutine first will find whether all the rows are filled with different digits,
- second will find whether all the columns are filled with different digits,
- Third will find out for each of the \(3*3\) grid if all the elements are unique.
- First 2 cases are trivially solvable by traversing the board horizontally and vertically.
- The main challenge comes when we need to check for individual \(3*3\) grids. To do that I find what is the mid point for each of the \(3*3\) grids. These are \(\{(1,1), (1,4), (1,7), \dots\}\) with 0 based indexing. Sitting at the mid point I do a little detour via the
detourfunction to cover the whole \(3*3\) grid and check for the uniqueness of the values.
- At the end our solution to the problem becomes true if it is
columnCorrectandrowCorrectandgridCorrect. Hence the following code:
Code
class Solution {
private:
unordered_map<char, bool> getTraveller() {
unordered_map<char, bool> traveller;
for (int i=1; i<=9; i++) {
char c = i + '0';
traveller[c] = false;
}
return traveller;
}
bool columnCorrect(vector<vector<char>>& board) {
for (int i=0; i<9; i++) {
unordered_map<char, bool> traveller = getTraveller();
for (int j=0; j<9; j++) {
if (board[j][i] != '.') {
if (traveller[board[j][i]]) {
return false;
} else {
traveller[board[j][i]] = true;
}
}
}
}
return true;
}
bool rowCorrect(vector<vector<char>>& board) {
// for each of the row create a traveller
// mark if some thing is not visited from 1-9
// else if already visited return false
for (int i=0; i<9; i++) {
unordered_map<char, bool> traveller = getTraveller();
for (int j=0; j<9; j++) {
if (board[i][j] != '.') {
if (not traveller[board[i][j]]) {
traveller[board[i][j]] = true;
} else {
return false;
}
}
}
}
return true;
}
pair<int, int> getMidFromGridIndex(int gridIndex) {
// all the grids are indexed 0-8. For a given grid number
// this returns the mid point of the grid
int row = (gridIndex/3)* 3 + 1;
int col = (gridIndex % 3) * 3 + 1;
return {row, col};
}
void detour(vector<vector<char>>& board, int row, int col, int limit, unordered_map<char, bool> &traveller, bool &possible) {
/* Recursive detour and check for the 3*3 grid as this [row-col] begin middle*/
if (limit > 1) return;
char valueHere = board[row][col];
if (traveller[valueHere] and valueHere != '.') {
possible = false;
return;
}
traveller[valueHere] = true;
detour(board, row+1, col, limit+1, traveller, possible);
detour(board, row, col-1, limit+1, traveller, possible);
detour(board, row, col+1, limit+1, traveller, possible);
detour(board, row-1, col, limit+1, traveller, possible);
detour(board, row+1, col+1, limit+1, traveller, possible);
detour(board, row+1, col-1, limit+1, traveller, possible);
detour(board, row-1, col-1, limit+1, traveller, possible);
detour(board, row-1, col+1, limit+1, traveller, possible);
}
bool gridCorrect(vector<vector<char>>& board) {
// there is total of 9 grids, we need to check all of the grids
for (int gridID=0; gridID<9; gridID++) {
pair<int, int> midPoint = getMidFromGridIndex(gridID);
// create a new traveller
unordered_map<char, bool> traveller = getTraveller();
bool possible = true;
detour(board, midPoint.first, midPoint.second, 0, traveller, possible);
// if not possible then return false other wise go to the next grid
if (not possible) return false;
}
return true;
}
public:
bool isValidSudoku(vector<vector<char>>& board) {
return columnCorrect(board) and rowCorrect(board) and gridCorrect(board);
}
};
Sort the Array
Find the problem on Codeforces \(\to\)
Problem Statement
Being a programmer, you like arrays a lot. For your birthday, your friends have given you an array a consisting of \(n\) distinct integers.
Unfortunately, the size of a is too small. You want a bigger array! Your friends agree to give you a bigger array, but only if you are able to answer the following question correctly: is it possible to sort the array \(a\) (in increasing order) by reversing exactly one segment of \(a\)? See definitions of segment and reversing in the notes.
Input The first line of the input contains an integer \(n (1 \leq n \leq 10^5)\) — the size of array \(a\).
The second line contains n distinct space-separated integers: \(a[1], a[2], ..., a[n] (1 \leq a[i] \leq 10^9)\).
Output Print "yes" or "no" (without quotes), depending on the answer.
If your answer is "yes", then also print two space-separated integers denoting start and end (start must not be greater than end) indices of the segment to be reversed. If there are multiple ways of selecting these indices, print any of them.
Examples
Input:
3
3 2 1
Output:
yes
1 3
Explain: You can reverse the entire array to get [1, 2, 3], which is sorted.
Approach
- Find one decreasing-increasing segment. Then check if first element of decreasing segment is less than first element of the increasing segment. Then it is possible to reverse the decreasing segment and get the sorted order.
- If there is more than one increasing and decreasing segment, then it is not possible.
- Otherwise it is possible to reverse the decreasing segment and get the sorted order.
Code
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int findFirstDecrementPoint(vector<int> &numbers) {
for (int i = 0; i < numbers.size() - 1; i++) {
if (numbers[i] > numbers[i + 1]) {
return i;
}
}
return -1;
}
bool moreThanOneIncrementDecrementSegment(int firstIncrementPoint, vector<int> &numbers) {
for (int i = firstIncrementPoint + 1; i < numbers.size() - 1; i++) {
if (numbers[i] > numbers[i + 1]) {
return true;
}
}
return false;
}
pair<pair<int, int>, string> findIfSortingPossible(vector<int> &numbers) {
int firstDecrementPoint = findFirstDecrementPoint(numbers);
if (firstDecrementPoint == -1) {
return {{1, 1}, "yes"};
}
// from this firstDecrement point find what is the first increment point
int firstIncrementPoint = -1;
for (int i = firstDecrementPoint; i < numbers.size() - 1; i++) {
if (numbers[i] < numbers[i + 1]) {
// this is the first increment point
firstIncrementPoint = i;
break;
}
}
if (firstIncrementPoint == -1) {
// all are decreasing, there is no increment point later
// so check if last number is > the number at decrement point;
if (firstDecrementPoint == 0) {
// this means the entire array is reversing
return {{1, numbers.size()}, "yes"};
} else if (numbers.back() > numbers[firstDecrementPoint - 1]) {
// this means here reversing decrement segment is possible
return {{firstDecrementPoint + 1, numbers.size()}, "yes"};
}
} else {
if (moreThanOneIncrementDecrementSegment(firstIncrementPoint, numbers)) {
return {{0, 0}, "no"};
}
if (numbers[firstIncrementPoint + 1] > numbers[firstDecrementPoint]) {
return {{firstDecrementPoint + 1, firstIncrementPoint + 1}, "yes"};
}
}
return {{0, 0}, "no"};
}
int main() {
int size;
cin >> size;
vector<int> numbers(size);
for (int i = 0; i < size; i++) {
cin >> numbers[i];
}
pair<pair<int, int>, string> answer = findIfSortingPossible(numbers);
cout << answer.second << endl;
if (answer.first.first)
cout << answer.first.first << " " << answer.first.second << endl;
return 0;
}
Greatest Common Divisor of Strings
Find the problem on Leetcode \(\to\)
For two strings s and t, we say "t divides s" if and only ifs = t + ... + t(i.e.,t` is concatenated with itself one or more times).
Given two strings str1 and str2, return the largest string x such that x divides both str1 and str2.
Example
Input: str1 = "ABCABC", str2 = "ABC"
Output: "ABC"
Input: str1 = "ABABAB", str2 = "ABAB"
Output: "AB"
Input: str1 = "LEET", str2 = "CODE"
Output: ""
Approach
- Find all the prefix of the shorter string,
- Then for each of the prefixes find if that is both a valid divisor of
str1andstr2. Find the greatest common divisor using loops.
Code
class Solution {
public:
vector<string> findPrefixes(string str) {
string pref = "";
int size = str.size();
vector<string> prefixes;
for (int i = 0; i < size; i++) {
pref += str[i];
prefixes.push_back(pref);
}
return prefixes;
}
bool validDivisor(string str, string prefix) {
bool valid = true;
int size = prefix.size();
int index = 0;
for (char c:str) {
if (c == prefix[index]) {
index++;
index %= size;
} else {
valid = false;
break;
}
}
if (index > 0) valid = false;
return valid;
}
string gcdOfStrings(string str1, string str2) {
int size1 = str1.size();
int size2 = str2.size();
string currentCommonDivisor = "";
if (size1 < size2) {
vector<string> prefixList = findPrefixes(str1);
for (auto prefix:prefixList) {
bool validForString2 = validDivisor(str2, prefix);
bool validForString1 = validDivisor(str1, prefix);
if (validForString1 and validForString2) {
currentCommonDivisor = prefix;
}
}
} else {
vector<string> prefixList = findPrefixes(str1);
for (auto prefix:prefixList) {
bool validForString2 = validDivisor(str2, prefix);
bool validForString1 = validDivisor(str1, prefix);
if (validForString1 and validForString2) {
currentCommonDivisor = prefix;
}
}
}
return currentCommonDivisor;
}
};
Comments
This comments system is powered by GitHub Discussions