Stack Problems
Problem Index
- Nearest greater to right or Next Largest Element
- Next Greater Element I
- Nearest greater to left (NGEle)
- Nearest smaller to left (NSEle)
- Minimum Stack with extra space
- Stock Span Problem
- Maximum Area Histogram
- Max Area Rectangle under binary matrix
- The Skyline problem
- Score of Parentheses
- Implement a stack with single queue
- Cd and pwd commands
Patterns of questions when to use a stacks.
Using Same concept
- Nearest greater to right or Next Largest Element
- Nearest greater to left
- Nearest smaller to right
- Nearest smaller to left
Using the code from the previous concept
- Stock Span Problem
- Maximum area of histgram
Using the code from the previous two concepts
- Max area of rectangle in binary matrix
Other good problems on stack
- Rain water trapping
- Implement Min stack with or without extra space
For problems with array think of using stacks, also for problems that uses nested for loops and the inner for loop is dependent upon the outer for loop like the following
for (int i; i< n; i++){
for(int j; j -> 0 to i; j++);
for(int j; j -> i to 0; j--);
for(int j; j -> i to n; j++);
for(int j; j -> n to i; j--);
}
Nearest greater to right or Next Largest Element
Problem statement
Given an array, print the Next Greater Element to the right for every element. The Next greater Element for an element x is the first greater element on the right side of x in the array. Elements for which no greater element exist, consider the next greater element as -1.
Examples
Input Array: [4, 5, 2, 25]
Input Array: [1, 3, 2, 4]
Brute Force approach
- Traverse the whole array, for each element at i, traverse from i+1 to at worst n to get the first element that is greater than the element at i.
- This is a pattern for nested
for loopsand the innerforloop is dependent upon the outerforloop. So we can use a stack to optimize the solution.
def brute_force_NGE(array: list[int]) -> None:
for i in range(len(array)):
for j in range(i+1, len(array)):
# ...
pass
# ...
pass
return None
Optimized solution with Stacks
Stack implementation
from collections import deque
class Stack:
def __init__(self):
self.container = deque()
def pop(self):
return self.container.pop()
def push(self, value):
self.container.append(value)
def tos(self):
return self.container[-1] if self.container else -1
def isEmpty(self):
return len(self.container) == 0
Optimized apporach with stacks
- We start from the very last, and maintain a stack.
- if the stack is empty means that there is no element that is just greater to the right of this element so return -1
- if we don't find anything then push the element onto the stack.
- if the
a[i]element is < the top of the stack means thattos()is the next greater element, - if the
a[i]is > the top of the stack then wepop()from the stack to find if there is any element > thea[i], if not return -1.
def NGE(array):
stack = Stack()
returnarray = []
end = len(array) - 1
while end >= 0: # unitl we reach to the front
if stack.isEmpty():
stack.push(array[end])
returnarray.append(-1)
else:
while not stack.isEmpty() and stack.tos() <= array[end]:
stack.pop()
if stack.isEmpty():
stack.push(array[end])
returnarray.append(-1)
elif stack.tos() > array[end]:
returnarray.append(stack.tos())
stack.push(array[end])
end -= 1
return returnarray[::-1]
console.print(NGE([3, 2, 1, 0, 2, 4, 2, 6, 9]))
console.print(NGE([3, 2, 11, -0.4, 2, 4, 2, 6, 91]))
Next Greater Element I
Find the problem on Leetcode \(\to\)
Problem Statement
The next greater element of some element \(x\) in an array is the first greater element that is to the right of \(x\) in the same array.
You are given two distinct 0-indexed integer arrays nums1 and nums2, where nums1 is a subset of nums2.
For each 0 <= i < nums1.length, find the index j such that nums1[i] == nums2[j] and determine the next greater element of nums2[j] in nums2. If there is no next greater element, then the answer for this query is \(-1\).
Return an array ans of length nums1.length such that ans[i] is the next greater element as described above.
Example
Input: nums1 = [4,1,2], nums2 = [1,3,4,2]
Output: [-1,3,-1]
Explanation: The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = [1,3,4,2]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = [1,3,4,2]. The next greater element is 3.
- 2 is underlined in nums2 = [1,3,4,2]. There is no next greater element, so the answer is -1.
Input: nums1 = [2,4], nums2 = [1,2,3,4]
Output: [3,-1]
Explanation: The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = [1,2,3,4]. The next greater element is 3.
- 4 is underlined in nums2 = [1,2,3,4]. There is no next greater element, so the answer is -1.
Approach
We'll use the up above technique (usage of stacks) to find the next greater element to the right.
Code
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
std::unordered_map<int, int> nge;
vector<int> stack;
int last = nums2.back();
stack.push_back(last);
nge[last] = -1;
int size = nums2.size();
for (int i = size - 2; i >= 0; i--) {
while (not stack.empty() and nums2[i] > stack.back()) {
stack.pop_back();
}
if (stack.empty()) {
nge[nums2[i]] = -1;
} else if (nums2[i] < stack.back()) {
nge[nums2[i]] = stack.back();
}
stack.push_back(nums2[i]);
}
vector<int> answer;
for (int i:nums1) {
answer.push_back(nge[i]);
}
return answer;
}
};
Nearest greater to left (NGEle)
Problem statement
Given an array, print the Next Greater Element to the left for every element. The Next greater Element for an element x is the first greater element on the left side of x in the array. Elements for which no greater element exist, consider the next greater element as -1.
Examples
Input Array: [4, 5, 2, 25]
Input Array: [1, 3, 2, 4]
Approach
- Similar to the NGE but we start from the left because we have to operate on the left sub-array.
from collections import deque
class Stack:
def __init__(self):
self.s = deque()
def push(self, value):
self.s.append(value)
def pop(self):
return self.s.pop()
def tos(self):
return self.s[-1]
def isEmpty(self):
return len(self.s) == 0
def NGEle(array: list[int]):
last = len(array)
out = []
stack = Stack()
for i in range(0, last):
if stack.isEmpty():
stack.push(array[i])
out.append(-1)
else:
while not stack.isEmpty() and stack.tos() < array[i]:
stack.pop()
if stack.isEmpty():
stack.push(array[i])
out.append(-1)
elif stack.tos() > array[i]:
out.append(stack.tos())
stack.push(array[i])
return out
print(NGEle([4, 5, 2, 0.5, 25]))
print(NGEle([1]), NGEle([]), NGEle([-13, -12, -11, -10])) # Some corner cases
Nearest smaller to left (NSEle)
Problem statement
Given an array, print the Next Greater Element to the left for every element. The Next greater Element for an element x is the first greater element on the left side of x in the array. Elements for which no greater element exist, consider the next greater element as -1.
Examples
Input Array: [4, 5, 2, 25]
Input Array: [1, 3, 2, 4]
Approach
- Drop the bad Brute force approach, we should use a stack
- Start from the begining and traverse throught the array from \(0 \to \mathcal{N}\)
- For each element check the left sub-array using a stack.
- Pop elements out of the stack if they are greater and push the current element.
- return -1 for empty stack and
tos()if we find elements lesser (i.e. the lesser element).
from collections import deque
class Stack:
def __init__(self):
self.s = deque()
def pop(self):
return self.s.pop()
def isEmpty(self):
return len(self.s) == 0
def push(self, value):
self.s.append(value)
def tos(self):
return self.s[-1]
def NSEle(array: list[int]) -> list[int]:
end = len(array)
stack = Stack()
out = []
for i in range(0, end):
if stack.isEmpty():
stack.push(array[i])
out.append(-1)
else:
while not stack.isEmpty() and (stack.tos() > array[i]):
stack.pop()
if stack.isEmpty():
stack.push(array[i])
out.append(-1)
elif stack.tos() < array[i]:
out.append(stack.tos())
stack.push(array[i])
return out
print(NSEle([4, 5, 2, 25]))
print(NSEle([1, 3, 2, 4]))
print(NSEle([4, 5, 2, 0.5, 25]))
print(NSEle([-13, -12, -11, -10]))
print(NSEle([1]), NSEle([]), NSEle([13, 12, 11, 10])) # Some corner cases
Minimum Stack with extra space
Problem Statement
Implement a stack with the following methods:
MinimumStack()constructs a new instance of a minimum stackappend(int val)appends val to the stackpeek()retrieves the last element in the stackmin()retrieves the minimum value in the stackpop()pops and returns the last element in the stack Each method should be done in \(\mathcal{O}(1)\) time. You can assume that for peek, min and pop, the stack is non-empty when they are called.
Constraints
\(n ≤ 100000\) where n is the number of calls to append, peek, min, and pop.
Approach
- We'll use a two stack approach, one to keep track of all the stack elements (
self.container) and an auxiliary stack to keep track all the minimum elements. - Whenever we find a new
minelement we'll push it into theself.auxstack. - When we find
pop()and find sametos()forself.containerandself.auxmeans that the current minimum element is beingpoppedoff. So wepop()from both.
class MinimumStack:
def __init__(self):
self.container = deque()
self.aux = deque()
def append(self, val):
self.container.append(val)
if len(self.aux) == 0:
self.aux.append(val)
elif len(self.aux) > 0 and val < self.aux[-1]:
self.aux.append(val)
def peek(self):
return self.container[-1]
def min(self):
return self.aux[-1]
def pop(self):
if self.aux[-1] == self.container[-1]:
k = self.container.pop()
self.aux.pop()
return k
else:
return self.container.pop()
#include <iostream>
#include <vector>
using namespace std;
class MinStack{
private:
vector<int> stack;
vector<int> auxStack;
int ClassPrivateSize;
public:
MinStack(){
ClassPrivateSize = 0;
}
int size(){
return ClassPrivateSize;
}
void push(int value){
if (ClassPrivateSize == 0){
stack.push_back(value);
auxStack.push_back(value);
ClassPrivateSize += 1;
}else{
if (value < auxStack.back()){
stack.push_back(value);
auxStack.push_back(value);
}else{
stack.push_back(value);
}
ClassPrivateSize += 1;
}
}
int pop(){
if (ClassPrivateSize == 0){
throw runtime_error("pop(): Empty Stack");
}else{
if (auxStack.back() == stack.back()){
int value = stack.back();
auxStack.pop_back();
stack.pop_back();
return value;
}else{
int value = stack.back();
stack.pop_back();
return value;
}
ClassPrivateSize -=1;
}
}
bool isEmpty() const{
if (ClassPrivateSize == 0){
return true;
}
return false;
}
int min(){
return auxStack.back();
}
int peek() {
return stack.back();
}
};
Time Complexity
push()takes \(\mathcal{O}(1)\)pop()takes \(\mathcal{O}(1)\)min()takes \(\mathcal{O}(1)\)peek()takes \(\mathcal{O}(1)\)
Space Complexity
At the very worst total space complexity is \(\mathcal{O}(N)\)
Stock Span Problem
Problem Statement
Equivalent problems are on LeetCode and GeeksForGeeks
- The stock span problem is a financial problem where we have a series of n daily price quotes for a stock and we need to calculate span of stock’s price for all n days.
- The span Si of the stock’s price on a given day i is defined as the maximum number of consecutive days just before the given day, for which the price of the stock on the current day is less than its price on the given day.
Example testcase
For example, if an array of \(7\) days prices is given as \(\{100, 80, 60, 70, 60, 75, 85\}\), then the span values for corresponding 7 days are \(\{1, 1, 1, 2, 1, 4, 6\}\). For simplicity,
- For day \(1\), no days are before this day that has more than this day's stock value so return \(1\)
- For day \(3\), no days are before this day that has more than this day's stock value so return \(1\)
- For day \(4\), there is exactly one day that has more than this day's stock value so return \(1 + 1 = 2\)
- For the last day stock value is \(85\) and there is total 5 days before this day which has less stock value: \(\{75, 60, 70, 60, 80\}\). So return \(5+1 =6\)
Approach
If we look closely, this problem is really the NGEle problem (Nearest greatest to the left), now instead of returning that we find/count how much (long) ago that nearest smallest was?
So the apporach should be
- Figure out the NGEle first with stack in \(O(\mathcal{N})\) space.
- Now use as much \(O(\mathcal{N})\) space as possible beacuse you can not reduce it, so keep the program simple.
- Finally instead of the NGEle array we return the NGEle array along with what was the index number of that NGEle element using a vector of pairs.
- Now for the
stockSpan()function we will return the difference between the position of current element and the position of the NGEle element.

#include <iostream>
#include <vector>
using namespace std;
vector<pair<int, int>> NGEle(vector<int> vect){
// Return a pair with NGEle and the position of the NGEle.
vector<pair<int, int>> out;
// While storing the values into stack just add the current index to keep track
// of where the NGEle is located.
vector<pair<int, int>> stack;
// Common NGEle Code [it's the same lolzzzzz].
int index = 0;
for (int element:vect){
if (stack.size() == 0){
out.push_back({-1, -1});
stack.push_back({element, index});
}else{
while ((stack.size() != 0) && (stack.back().first < element)){
stack.pop_back();
}
if (stack.size() == 0){
out.push_back({-1, index});
stack.push_back({element, index});
}else if (stack.back().first > element){
out.push_back({stack.back().first,stack.back().second});
stack.push_back({element, index});
}
}
index++;
}
return out;
}
vector<int> stockSpan(vector<int> marketCap){
// find NGEle Values for each day along with their indexes.
vector<pair<int, int>> ngele = NGEle(marketCap);
vector<int> out;
int idx = 0;
// Now for each element find the distance between it and it's NGEle.
for (auto i: ngele){
if (i.second != -1){
out.push_back(idx - i.second + 1);
}else{
out.push_back(1);
}
idx++;
}
return out;
}
Let's test the code out. Run the following code to see the code working.
int main(){
vector<int> v = {100, 70, 85, 59, 15, 60, 87};
vector<pair<int, int>> ngele = NGEle(v);
vector<int> stkspan = stockSpan(v);
cout << "Market CAP" <<endl;
for (auto j: v)
cout << j << " ";
cout << endl;
cout << endl;
// ngele Array
for (auto i: ngele){
cout << i.first << " from: " << i.second << "\n";
}
cout << endl;
cout << "Stock Span" <<endl;
for (auto h: stkspan)
cout << h << " ";
cout << endl;
return 0;
}
Time Complexity
At the very worst case time complexity is \(O(\mathcal{N})\) because we are traversing the marketCap vector only once during the subroutine NGEle() and once in the subroutine stockSpan().
Space Complexity
Space complexity is \(O(\mathcal{N})\).
Maximum Area Histogram
Problem Statement
Given an array of integers heights representing the histogram's bar height where the width of each bar is \(1\), return the area of the largest rectangle in the histogram.
Examples
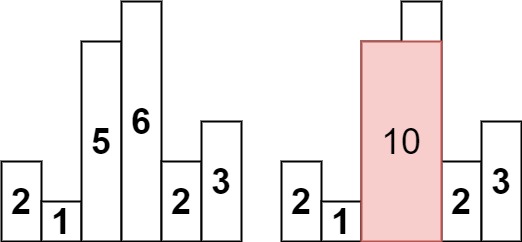
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation:
The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
Thought process
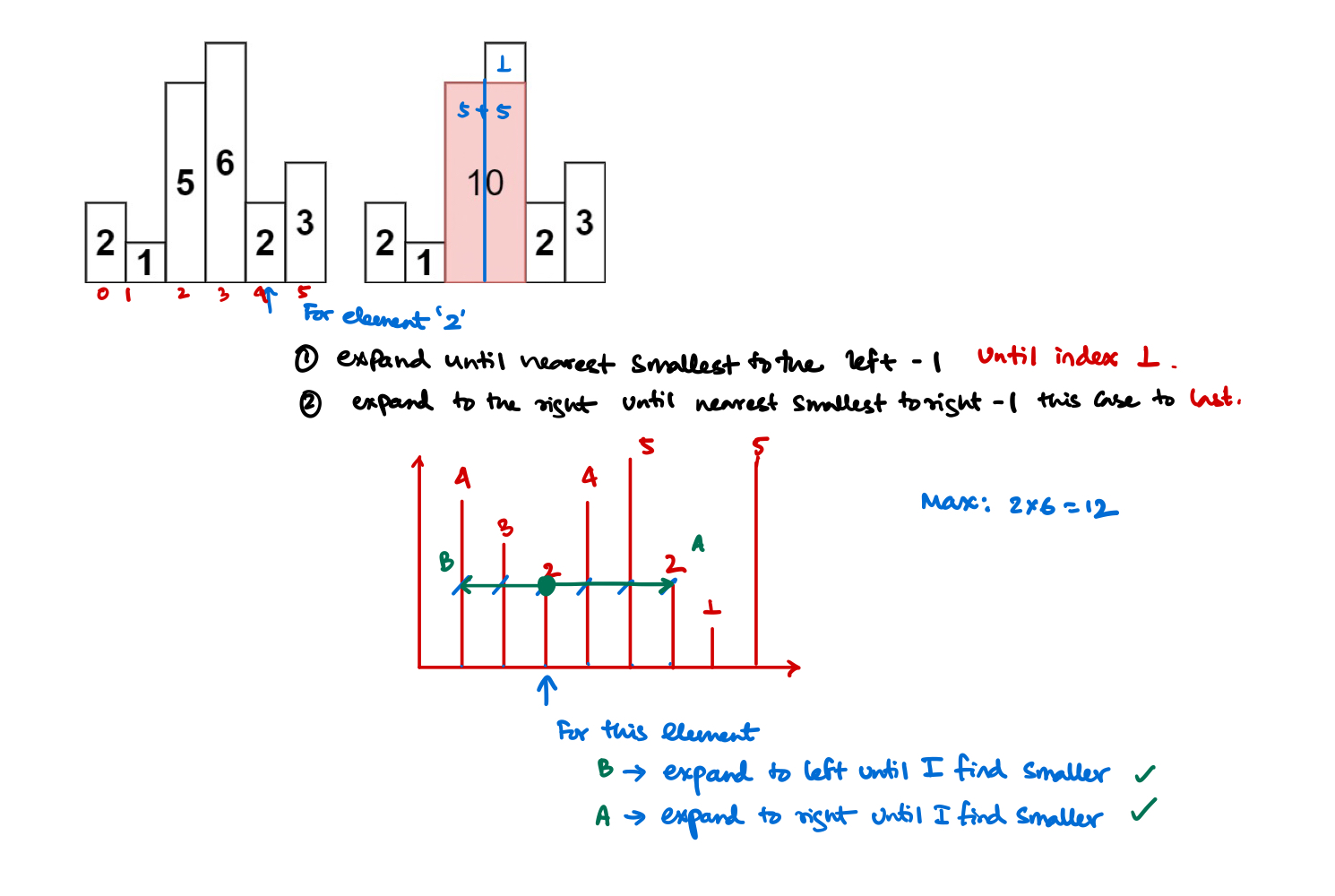
Approach
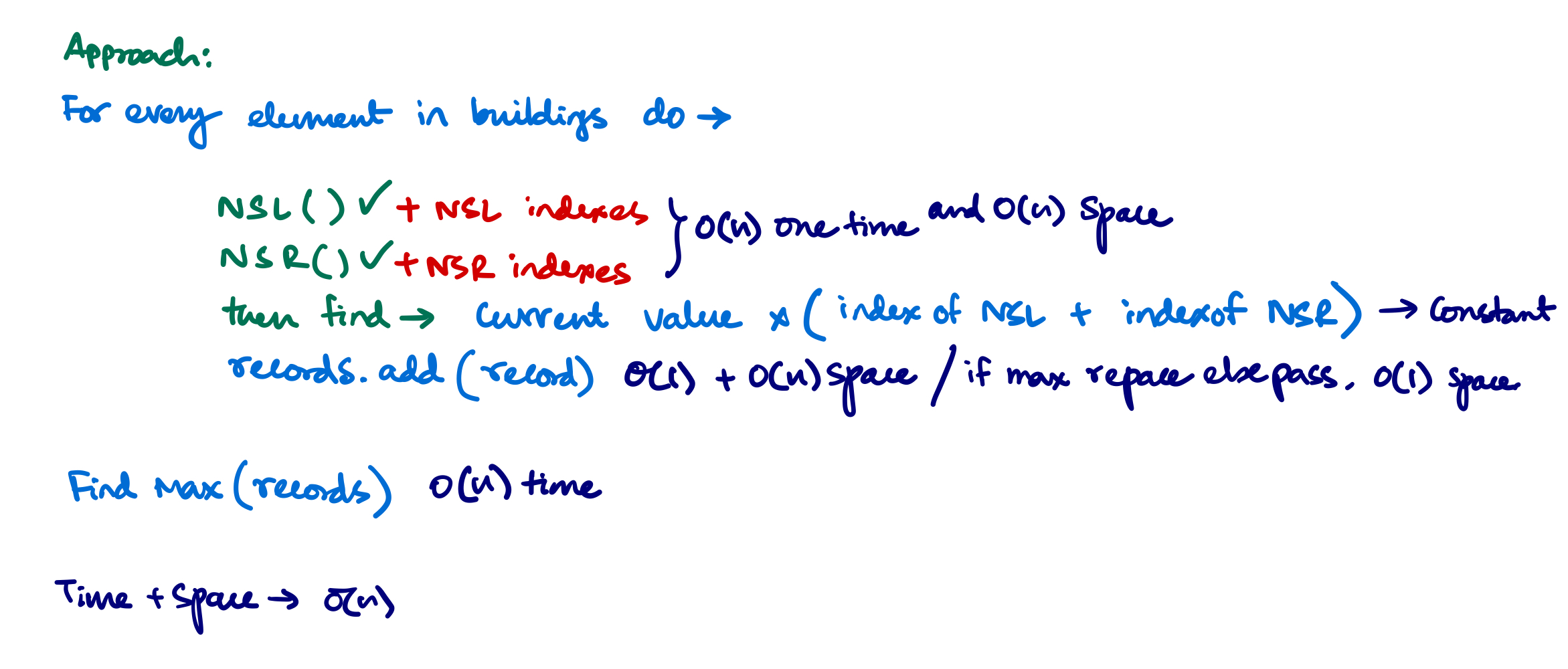
Time and Space complexity
\(O(\mathcal{N})\) time and space is taken.
Code
Subroutines
Two subroutines are needed \(\to\) and these are NSEle and NSR. Neareast smaller to the left and neareast smaller to the right.
NSR (NSE, Nearest smaller to the Right) implementation
#include <iostream>
#include <vector>
using std::vector;
using std::pair;
vector<pair<int, int>> NSE(vector<int> vect){
// Nearest smallest to the right
// finds and returns NSE array pair.first -> value
// pair.second -> index of the NSE element
vector<pair<int, int>> out;
vector<pair<int, int>> stack;
int last = vect.size() - 1;
while (last != -1){
if (stack.size() == 0){
out.push_back({-1, -1});
stack.push_back({vect[last], last});
}else{
while ((stack.size() != 0) && (stack.back().first >= vect[last])){
stack.pop_back();
}
if (stack.size() == 0){
out.push_back({-1, -1});
stack.push_back({vect[last], last});
}else if (stack.back().first < vect[last]){
out.push_back({stack.back().first, stack.back().second});
stack.push_back({vect[last], last});
}
}
last--;
}
return out;
}
NSEle (Nearest smaller to the left) implementation
vector<pair<int, int>> NSEle(vector<int> vect){
vector<pair<int, int>> out;
vector<pair<int, int>> stack;
int start = 0;
while (start != vect.size()){
if (stack.size() == 0){
out.push_back({-1, -1});
stack.push_back({vect[start], start});
}else{
while ((stack.size() != 0) && (stack.back().first >= vect[start])){
stack.pop_back();
}
if (stack.size() == 0){
out.push_back({-1, -1});
stack.push_back({vect[start], start});
}else if (stack.back().first < vect[start]){
out.push_back({stack.back().first, stack.back().second});
stack.push_back({vect[start], start});
}
}
start++;
}
return out;
}
The main function maxAreaHistogram()
void maxAreaHistogram(vector<int> v){
vector<int> out;
vector<pair<int, int>> nsr = NSE(v);
// NSR has to-be reverse because we started from the begining
std::reverse(nsr.begin(), nsr.end());
vector<pair<int, int>> nsele = NSEle(v);
int currentMax = -1;
int index = 0;
int currentArea = 0;
for (int i:v){
if ((nsr[index].first != -1) && (nsele[index].first != -1)){
// Both upper and lower bound is within the array
// Start from left bound + 1
// end at the upper bound - 1 (don't cosinder the upper bound bcz it's smaller)
currentArea = i * ((nsr[index].second - 1) - (nsele[index].second + 1) + 1);
}else if ((nsr[index].first == -1) && (nsele[index].first != -1)){
// right side -> -1 no smaller element to the right
// Start from left bound + 1, (don't consider the left bound)
// end at last
currentArea = i * (v.size()-1 - (nsele[index].second + 1) + 1);
}else if ((nsele[index].first == -1) && (nsr[index].first != -1)){
// No bound to the left
// So from index zero -> the upper bound
currentArea = i * (nsr[index].second - 1 + 1);
}else{
// No bound at all -> size * magnitude
currentArea = i * (v.size());
}
out.push_back(currentArea);
index++;
}
for (auto value:out)
std::cout << BOLDBLUE << value << " ";
std::cout << std::endl;
}
Testing the code out
int main(){
// testsForNSE();
// testsForNSEle();
vector<int> v = {1, 2, 3, 1, 2, 3, 4, 5, 5, 5};
std::cout << BOLDCYAN << "TEST CASE 1" << RESET << std::endl;
maxAreaHistogram(v);
vector<int> v1 = {2,1,5,6,2,3};
std::cout << BOLDYELLOW << "TEST CASE 2" << RESET << std::endl;
maxAreaHistogram(v1);
vector<int> v2 = {2,4,1,4,4,5};
std::cout << BOLDMAGENTA << "TEST CASE 4" << RESET << std::endl;
maxAreaHistogram(v2);
vector<int> v12 = {5,5,5,5,5,2,4,2,1};
std::cout << BOLDGREEN << "TEST CASE 3" << RESET << std::endl;
maxAreaHistogram(v12);
vector<int> v23 = {3,2,1};
std::cout << BOLDMAGENTA << "TEST CASE 4" << RESET << std::endl;
maxAreaHistogram(v23);
vector<int> v231 = {10, 9, 8, 7};
std::cout << BOLDRED << "TEST CASE 4" << RESET << std::endl;
maxAreaHistogram(v231);
vector<int> v2321 = {7,8,9,10};
std::cout << BOLDMAGENTA << "TEST CASE 4" << RESET << std::endl;
maxAreaHistogram(v2321);
return 0;
}
Output
TEST CASE 1
10 4 3 10 12 15 16 15 15 15
TEST CASE 2
2 6 10 6 8 3
TEST CASE 4
4 4 6 12 12 5
TEST CASE 3
25 25 25 25 25 16 4 16 9
TEST CASE 4
3 4 3
TEST CASE 4
10 18 24 28
TEST CASE 4
28 24 18 10
Max Area Rectangle under binary matrix
Problem Statement
Given a binary matrix \(\mathcal{M}\) find out what is the maximum area of the rectangle \(R\), where all elements in \(R = 1\)

Explanation
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.
Constraints:
rows==matrix.lengthcols==matrix[i].length- 1 <=
row, cols<= 200 matrix[i][j]is \(0\) or \(1\).
Approach
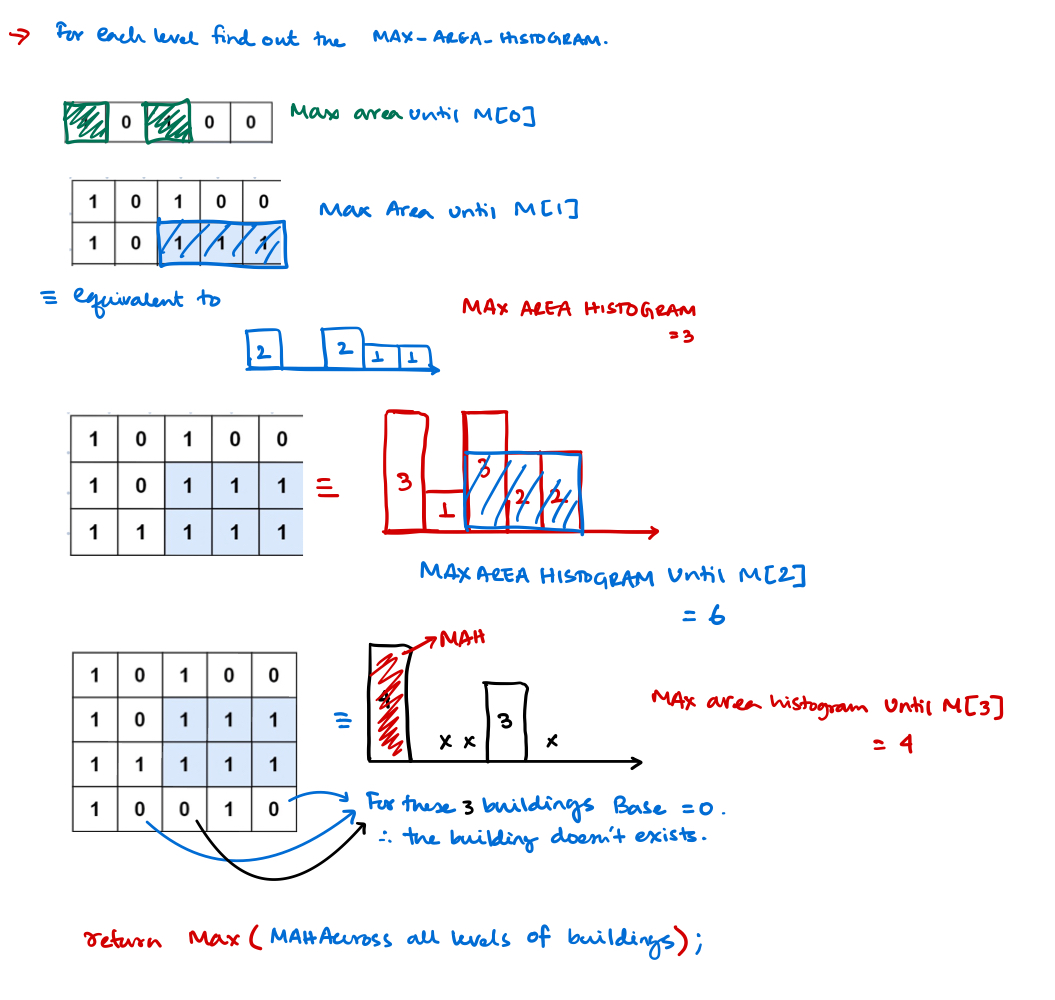
- We should start with creating histogram for each level.
- Then we call the
MAH()algorithm implemented in the previous question. - Then we find the maximum accross all levels.
The Skyline problem
Same Problem on Leetcode \(\to\)
Problem Statement
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.
Score of Parentheses
Problem Statement
Given a balanced parentheses string s, return the score of the string - "()" has score 1, - AB has score A + B, where A and B are balanced parentheses strings, - (A) has score 2 * A, where A is a balanced parentheses string.
Examples
Constraints
- \(2\) <=
s.length<= \(50\) sconsists of only'('and')'.sis always a balanced parentheses string.
Approach
- Using recursion because seems like a recursive problem with pattern of
return (what is inside of(what is inside of (what is inside))).
C++ code
class Solution {
private:
int globalTracker = 0;
public:
int scoreOfParentheses(string s) {
int score = 0;
// Using recursion bcz seems like a recursive problem
// return (what is inside of(what is inside of (what is inside)))
while(globalTracker < s.size() - 1){
char first = s.at(globalTracker);
globalTracker++;
char second = s.at(globalTracker);
if (first == '('){
if (second == ')'){
score = score + 1;
globalTracker++;
} else {
score = score + 2 *(scoreOfParentheses(s));
}
} else {
return score;
}
}
return score;
}
};
Implement a stack with single queue
Find the problem on leetcode
Problem Statement
Implement a last-in-first-out (LIFO) stack using only single queue. The implemented stack should support all the functions of a normal stack (push, top, pop, and empty). Implement the MyStack class
void push(int x)Pushes element \(x\) to the top of the stack.int top()Returns the element on the top of the stack.int pop()Removes the element on the top of the stack and returns it.boolean empty()Returns true if the stack is empty, false otherwise.
Apporach
It is easy to implement a stack with two queues. But the question requires us to use a single queue for storage. Our apporach will be the following:
Once a value comes to our stack we'll insert it into the internal queue, then from \(i \in \{0 \dots size - 1\}\) times we'll take the front of the queue and push it to the back of the queue. Then pop from the front of the queue. This will rearange the queue to have the data ordered like a stack.
Thus our queue.front() will return the element on the top of the stack and queue.pop() will pop the top of the stack.
Code
class MyStack {
public:
queue<int> q;
int size = 0;
MyStack() {}
void push(int x) {
size++;
q.push(x);
for (int i = 0; i < size - 1; i++) {
q.push(q.front());
q.pop();
}
}
int pop() {
int val = q.front();
q.pop();
size--;
return val;
}
int top() {
return q.front();
}
bool empty() {
return size == 0;
}
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
Cd and pwd commands
Problem Statement
Implement the Unix like cd and pwd commands.
- pwd of root should return /,
- cd /home/vasya will go to cd /home/vasya, then if we do cd /home/theroyakash it'll go to root and then go to home to theroyakash,
- cd /home/vasya and then cd home/theroyakash sends present working directory to cd /home/vasya/home/theroyakash, notice that second cd do not start with /.
Approach
Standard Stack approach.
Code
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;
/*
* Tokenise a string of path to individual folders
* eg. /home/theroyakash/go should return <home, theroyakash, go>
*/
vector<string> tokenize(string s, char delimeter) {
int size = s.size();
vector<string> tokens;
string current = "";
for (int i = 0; i < size; i++) {
if (s[i] == delimeter and current != "") {
tokens.push_back(current);
current = "";
} else if (s[i] != delimeter){
current += s[i];
}
}
tokens.push_back(current);
return tokens;
}
int main() {
int commands;
cin >> commands;
vector<string> stack;
while (commands--) {
string command;
cin >> command;
if (command == "pwd") {
if (stack.empty()) {
cout << "/" << endl;
continue;
}
for (int i = 0; i < stack.size(); i++) {
if (i == 0 and stack[i][0] != '/') {
cout << "/";
}
cout << stack[i] << "/";
}
cout << endl;
}
if (command == "cd") {
string directoryString;
cin >> directoryString;
if (directoryString[0] == '/') {
stack.clear();
}
vector<string> tokenizedDirectory = tokenize(directoryString, '/');
for (auto directory : tokenizedDirectory) {
// cout << directory << endl;
if (directory != "..") {
stack.push_back(directory);
} else {
stack.pop_back();
}
}
}
}
return 0;
}
Comments
This comments system is powered by GitHub Discussions